Теоретическое кривое распределение
Cтраница 2
Последний способ построения кривых иР ( 2рг) требует решения следующих двух задач: выбора типа теоретических кривых распределения и оценки неизвестных параметров этих кривых на основе рядов прошлых наблюдений. [16]
Для одномерных процессов в гидрологии функции распределения исследовались на протяжении многих лет, и в настоящее время имеется несколько теоретических кривых распределения вероятностей, которые используются в гидрологических расчетах. В СССР наиболее употребительным являются двух - и трехпа-раметрическое гамма-распределения. Первое из них часто называют кривой Пирсона III типа, второе - распределением Крицкого-Менке - л я. Принимая в качестве верхней границы оо, гидрологи считают, что такое событие имеет практически нулевую вероятность. [17]
Таким образом, сопоставляя числовые значения положения и площади первого максимума кривой распределения со значениями, вычисленными по предлагаемым моделям, можно судить о пространственном расположении атомов в исследуемом бинарном сплаве. Однако удовлетворительное совпадение теоретических кривых распределения с экспериментальными не всегда достигается. Нас же интересуют парциальные функции Qn ( R), Q2z ( R), Qi2 ( R) и Q2i ( R), описывающие структуру расплавов. [18]
Во-первых, достаточно один раз выбрать приемлемый тип теоретических кривых для каждой группы рек, и затем кривые распределения можно будет строить весьма просто. Во-вторых, для выбора теоретических кривых распределения можно использовать объединенные данные наблюдений по нескольким гидрологически сходным рекам, увеличивая этим самым период прошлых стоковых наблюдений. В-третьих, при использовании теоретических кривых облегчается оценка погрешностей построения функций распределения, в частности, погрешностей оценки неизвестных параметров распределения. И, наконец, облегчается построение функций перехода, управляющих марковским процессом. [19]
Кривая распределения частот, найденная в результате серии испытаний, называется экспериментальной. Получив такую кривую, исследователь обычно проверяет, не является ли она близкой к какому-либо типу теоретических кривых распределения, хорошо изученных в теории вероятностей. Такое сравнение нередко позволяет сделать определенные выводы относительно тех закономерностей, которые обусловили найденное экспериментальное распределение. [20]
К вопросу О том, какому закону подчиняется распределение погрешностей ( или размеров) при том или ином способе обработки, можно подойти двумя методами. Первый метод основан на измерении достаточно большого числа деталей и выявлении той из известных в математической статистике теоретических кривых распределения, к которой ближе всего подходит действительное распределение погрешностей или размеров обработанных деталей. [21]
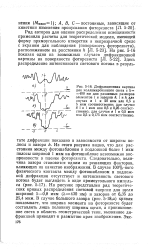
Кейс испытал 200 образцов в виде двусторонних лопаток из резин на основе натурального каучука и БСК, наполненных канальной сажей, при скорости растяжения 500 мм ] мин, по-видимому, при комнатной температуре. Гистограммы данных, полученных для обеих резин, показаны на рис. 40, на котором для сравнения приведены теоретические кривые распределения. [22]
 |
Дифракционная картина для коллимированного света с Я, 400 нм для различных размеров элементов / и зазоров А. / и h для случая а 1 и 20 мкм или 0 5 и. [23] |
Из этого рисунка видно, что для расстояния между фотошаблоном и подложкой более 1 мкм полосы шириной 1 мкм на фотошаблоне невозможно воспроизвести в пленке фоторезиста. Следовательно, величина зазора становится одним из решающих факторов, влияющих на качество изображения. На рисунке представлен ряд теоретических кривых распределения световой энергии для щели шириной 5 - 0 8 мкм ( А 430 нм) и зазоров от 6 35 до 25 4 мкм. В случае большого зазора ( рис. 5 - 18 а) кривая показывает, что ширина элемента на фоторезисте будет составлять лишь половину ширины щели, а проникновение света в область геометрической тени, вызванное дифракцией приводит к размытию края изображения. [24]
Распределение локальных скоростей в точках обвода профиля существенно зависит от формы вогнутой и выпуклой поверхностей, а также от геометрических и режимных параметров решетки. Увеличение кривизны на выпуклых участках профиля приводит к увеличению скорости и наоборот. При скачкообразном изменении кривизны, например в точках сопряжения дуг окружностей, теоретические кривые распределения давлений и скоростей претерпевают разрыв. Поэтому обводы профиля современных решеток выполняют с плавно изменяющейся кривизной. [25]
Если расчет точности должен быть выполнен для изготовляемых приборов или аналогичных приборов, уже находящихся в производстве, то отбирают часть деталей, попадающих на сборку приборов, и их тщательно измеряют. На основании числовых результатов измерения могут быть найдены известными способами практические кривые распределения отклонений, а по ним выбраны теоретические кривые распределения, согласующиеся с практическими данными. [26]
Испускание распыляемого материала поверхностью поликристаллических и аморфных мишеней в случае падения ионов по нормали к поверхности достаточно хорошо аппроксимируется законом косинуса ( см. гл. Следовательно, некоторое количество материала, которое всегда испускается под достаточно малыми углами к поверхности катода, должно выходить из пространства, заключенного между плоскостями катода и подложки. Кроме того, в результате столкновений с атомами газа распыленные атомы могут несколько отклоняться в своем движении. Таким образом, вероятность того, что распыленные атомы не попадут на подложку, возрастает с увеличением расстояния катод - подложка и с удалением от центра катода. На рис. 7 приведено несколько теоретических кривых распределения распыленного материала в плоскости подложки для различных отношений диаметра катода к расстоянию между электродами. Кривые получены в предположении, что пространственное распределение выброса материала из катода подчиняется закону косинуса, что миграция материала по подложке отсутствует, что нет столкновений с атомами газа, и что катод имеет форму диска. [27]
Первый путь заключается в том, что колонка разбивается на действительное число элементарных слоев в соответствии с естественной плотностью сорбционных центров и расчет распределения веществ между сорбентом и раствором ведется на основании уравнения кинетики сорбции. Однако, вследствие того, что действительное число элементарных слоев очень велико ( порядка 10е - 107 на 1 см), вести такой расчет невозможно. Другой путь хотя и менее точен, но практически более приемлем. Он заключается в том, что неравновесные условия неявно учитываются путем уменьшения числа элементарных слоев. Эквивалентное число элементарных слоев в такой неравновесной колонке будет равно числу элементарных сорбционных актов, которые испытает в среднем одна частица в процессе движения ее через хроматографическую колонку. Распределение веществ в элементарном слое рассчитывается на основании изотерм сорбции. Сравнение экспериментальных и теоретических кривых распределения ионов в ионообменных колонках показывает, что теоретические кривые вполне удовлетворительно совпадают с экспериментальными кривыми, если расчет произведен для 10 - 100 элементарных слоев. [28]
Страницы: 1 2