Эмпирическое кривое распределение
Cтраница 1
Эмпирические кривые распределения строятся на клетчатках вероятности, отпечатанных типографским способом. Тип клетчатки вероятностей выбирается в соответствии с принятой аналитической функцией распределения вероятностей и полученного отношения С / СВ. [1]
Некоторые эмпирические кривые распределения размеров деталей, полученные в результате моделирования различных способов подналадки, показаны на рис. 3.7, где приняты следующие обозначения: первая буква - индекс способа подналадки ( см. выше); первая цифра - количество деталей п; вторая цифра - величина подналадочного импульса в микронах. Штриховой линией отмечено положение подналадочной границы. [2]
Аппроксимация асимметричных эмпирических кривых распределения ( I-IV типов) кривыми Пирсона III типа и модификацией гамма-распределения, предложенной С. Н. Крицким и М. Ф. Менкелем, с учетом величины и знака коэффициента асимметрии показывает удовлетворительную сходимость. [3]
Для построения эмпирических кривых распределения наивысших уровней используются ряды наблюдений наивысших уровней ( с восстановленными в случае необходимости пропусками в них), удлиненные по кривым связи соответственных уровней воды по другим водомерным постам, имеющим более продолжительный период наблюдений. [4]
На рисунке показаны эмпирические кривые распределения твердости сегментов. [5]
 |
Профили скоростей при ламинарном ( / и турбулентном течениях в трубах. [6] |
На рис. 6.24 приведены эмпирические кривые распределения скоростей турбулентного потока при разных числах Re, построенные по данным опытов Никурадзе, и для сравнения показана кривая, рассчитанная по формуле (6.29), соответствующей ламинарному режиму. Можно видеть, что профили скоростей для турбулентного потока более равномерные, чем для ламинарного. Это объясняется выравнивающим действием турбулентного перемешивания. [7]
Для сглаживания и экстраполяции эмпирических кривых распределения, как правило, применяется трехпараметрическое гамма-распределение при определенных отношениях Cs / Co. При надлежащем обосновании допускается применять биноминальную кривую распределения ( при С82С) или другие функции распределения вероятностей превышения. [8]
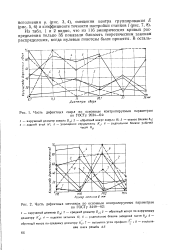 |
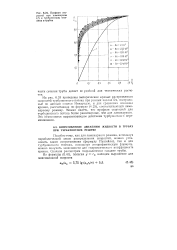
Часть дефектных сверл по основным контролируемым параметрам.| Часть дефектных метчиков по основным контролируемым параметрам. [9] |
Из табл. 1 и 2 видно, что из 116 эмпирических кривых распределения только 35 показали близость теоретическим законам распределения, когда нулевые гипотезы были приняты. [10]
Для сокращения незавершенного производства, образующегося при селективной сборке, строят эмпирические кривые распределения размеров соединяемых деталей. Если смещения центров группирования и кривые распределения размеров соединяемых деталей одинаковы и, например, соответствуют закону Гаусса, то количество деталей в одноименных группах будет одинаковым. Следовательно, только при идентичности кривых распределения сборка деталей одноименных групп ( рис. 111, д) устраняет образование незавершенного производства. Перейдем от деления допуска на равные части, выраженного в линейных величинах, к делению допуска на части, границы которых выражаются в о. Как видно, количество узлов, собранных из деталей второй группы, примерно в 4 раза больше, чем количество узлов, собранных из деталей первой или третьей групп. [11]
Для сокращения объемов незавершенного производства, образующегося при селективной сборке, строят эмпирические кривые распределения размеров соединяемых деталей. Если смещения центров группирования и кривые распределения размеров соединяемых деталей одинаковы и соответствуют, например, закону Гаусса, число собираемых деталей в одноименных группах одинаково. Следовательно, только при идентичности кривых распределения сборка деталей из одноименных групп ( рис. 11.8 5) устраняет образование незавершенного производства. [12]
Для сокращения объемов незавершенного производства, образующегося при селективной сборке, строят эмпирические кривые распределения размеров соединяемых деталей. Если смещения центров группирования и кривые распределения размеров соединяемых деталей одинаковы и соответствуют, например, закону Гаусса, то число собираемых деталей в одноименных группах будет одинаковым. Следовательно, только при идентичности кривых распределения сборка деталей одноименных групп ( рис. 9.9, д) устраняет образование незавершенного производства. [13]
Для сокращения объемов незавершенного производства, образующегося при селективной сборке, строят эмпирические кривые распределения размеров соединяемых деталей. Если смещения центров группирования и кривые распределения размеров соединяемых деталей одинаковы и соответствуют, например, закону Гаусса, то количество собираемых деталей в одноименных группах будет одинаковым. Следовательно, только при идентичности кривых распределения сборка детален одноименных групп ( см. рис. 9) устраняет образование незавершенно. [14]
Для сокращения объемов незавершенного производства, образующегося при селективной сборке, строят эмпирические кривые распределения размеров соединяемых деталей. Если смещения центров группирования и кривые распределения размеров соединяемых деталей одинаковы и соответствуют, например, закону Гаусса, число собираемых деталей в одноименных группах одинаково. Следовательно, только при идентичности кривых распределения сборка деталей из одноименных групп ( рис. 11.8 5) устраняет образование незавершенного производства. [15]
Страницы: 1 2 3