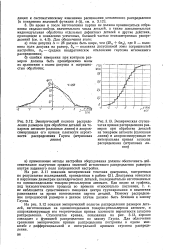
Эмпирическое кривое распределение

Cтраница 2

Анализ данных журналов учета машинного времени позволил также установить, что вид эмпирических кривых распределения по датам фактически затраченных на каждую операцию ресурсов ЭВМ зависит по конкретной задаче от объемов перерабатываемой информации. В связи с этим представляет интерес проведенный на основе имеющихся по 72 областным управлениям статистики данных математико-статистический анализ, целью которого являлось разбиение названных управлений статистики на несколько групп и выявление по каждой из них закономерностей распределения по датам затраченного машинного времени. [16]

Двухпараметрическими формулами, не претендующими, как правило, на универсальность, аппроксимируются эмпирические кривые распределения, полученные в результате анализов дисперсного состава определенных продуктов измельчения, выполненных определенными методами. Из них практическое распространение получили формулы Годэна - Андреева и Розина - Раммлера. Остальные формулы этой группы в практике дисперсионных анализов не применяются. [17]

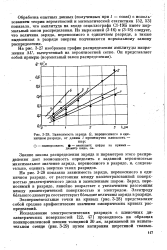Зависимость заряда Q, переносимого в единичном разряде, от длины I промежутка плоскость - шар. [18]

Экспериментальные точки на кривых ( рис. 3 - 28) представляют собой средние арифметические значения эмпирических кривых распределений. [19]

Статистическая обработка числовой информации производится, главным образом, для выявления закона распределения исследуемой случайной величины, определения его числовых характеристик, построения статистических рядов и эмпирических кривых распределения. [20]

Для изучения законов вариации вторичных случайных признаков статистических совокупностей ( коллективов), для нахождения их математического выражения с наибольшей степенью приближения к реальным фактам приходится строить специальные диаграммы, так называемые гистограммы, полигоны или эмпирические кривые распределения. Для этого поступают следующим образом. [21]

Для всех групп условий рассчитаны средние показатели ( см. табл. 26), а для некоторых из них ( L 6 лк, 300 лк, 64 лк, Н - 90 дБ при п 3) построены эмпирические кривые распределений ( см. рис. 36), позволяющие выбрать из данного ряда вариантов наилучший по показателю времени пребывания сигналов на приборе ( обработки оператором) с учетом одного из перечисленных выше критериев сравнения. [22]

Последующее микрометрирование деталей агрегатов или полнокомплектных автомобилей после их разборки с учетом сведений о сроках их службы позволяет получить необходимые данные для последующей обработки методами математической статистики с целью определения всех статистических характеристик износа: среднего значения, дисперсии, моды, медианы, эмпирических кривых распределения и соответствия их установленному закону. Анализ кривых распределения позволяет судить о том, как использовались автомобили и детали в процессе эксплуатации. [23]

Как показали многочисленные исследования, распределение погрешностей, изучение которых предусматривается при выполнении лабораторных работ, ближе всего соответствует закону нормального распределения. Построение эмпирических кривых распределения случайных погрешностей, подчиняющихся закону нормального распределения, обычно выполняется в следующей последовательности. [24]

Рассмотрим аппроксимацию на основе функций нормального распределения. Процесс выравнивания эмпирических кривых распределений рассмотрим на примерах применения для этой цели ряда уравнений, которыми часто пользуются в экономико-статистическом анализе. Начнем с уравнения нормального распределения, которое часто применяется в качестве стандарта, с которым сравнивают другие распределения и которое, как показано в следующей главе, имеет важное значение для решения задач выборочного наблюдения. [25]

Например, при малых температурах тела изучают главным образом инфракрасные лучи, а по мере повышения температуры излучение делается красноватым, оранжевым и, наконец, белым. На рис. 4.55 показаны эмпирические кривые распределения энергии излучения абсолютно черного тела по длинам волн при разных температурах: из них видно, что максимум спектральной плотности излучения при повышении температуры смещается в сторону коротких и волн. [26]

Например, при малых температурах тела излучают главным образом инфракрасные лучи, а по мере повышения температуры излучение делается красноватым, оранжевым и, наконец, белым. На рис. IV.79 показаны эмпирические кривые распределения энергии излучения абсолютно черного тела по длинам волн при разных температурах: из них видно, что максимум спектральной плотности излучения при повышении температуры смещается в сторону коротких волн. [27]

Однако, нередко приходится сталкиваться с такими явлениями, теоретические законы распределения которых еще не известны или недостаточно изучены. В таких случаях приходится ограничиваться подбором интерполяционных уравнений, которые достаточно точно воспроизводят эмпирические кривые распределения, а затем проверкой близости теоретических расчетов к действительности. [28]

Эмпирический полигон распределения размеров при обработке деталей на токарном автомате ( сплошная линия и аппроксимирующая его кривая плотности вероятности распределения Гаусса ( штриховая линия.| Эмпирическая ступенчатая кривая распределения размеров при обработке деталей на токарном автомате ( сплошная линия и аппроксимирующая ее интегральная кривая гауссова распределения ( штриховая линия. [29]

На рис. 3.12 показан эмпирический полигон распределения размеров деталей, изготовленных на одношпиндельном токарно-револьверном автомате, и аппроксимирующая его теоретическая кривая плотности вероятности гауссова распределения. Ступенчатая кривая, показанная на рис. 3.13, хорошо совпадает с функцией распределения по закону Гаусса. Для облегчения сравнения эмпирические кривые распределения построены в одном масштабе с дифференциальной и интегральной кривыми гауссова распределения. [30]

Страницы: 1 2 3