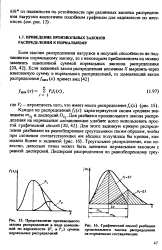
Треугольное распределение

Cтраница 2

Наименьшее значение вероятностей ошибок первого рода получается при равномерном распределении контролируемых величин и нормальном распределении погрешностей измерений, а наибольшее - при треугольном распределении контролируемых величин и равномерном распределении погрешностей измерений. [16]

График плотности ы2 ( х) представляет собой треугольник ( рис. 17), и поэтому распределение с плотностью и2 ( х) называется треугольным распределением. [17]

Эволюция плотности распределения вероятностей погрешности ТСХ с учетом погрешности квантования. [18]

Закон распределения плотности вероятности суммарной погрешности в этом случае определяется композицией законов распределения ее составляющих - равномерного и нормального для случая определения моментов времени, треугольного распределения Симпсона и нормального распределения Гаусса для случая измерения интервалов времени. Указанные композиции могут быть найдены с помощью регулярных методов теории вероятностей. [19]

Функции распределения обозначаются так: norm - нормальное распределение, unif - равномерное, expo - экспоненциальное, erln - обобщенное распределение Эрланга, beta - треугольное распределение, попе - интервал, являющийся детерминированной величиной. [20]

Для определения погрешности в конце диапазона канала нужно к составляющим погрешности ЦВ в конце диапазона канала с равномерным ( а1кЦВ 0 332 %) и экспоненциальным ( а2кЦВ 0 096 %) распределением прибавить мультипликативные погрешности от колебаний напряжения питания ( а ( / ( я у) 0 429 %) с треугольным распределением и погрешность от наводки ( анав 0 16 %) с арксинусоидальным распределением. [21]

Представление произвольного закона распределения в виде взвешен-ной по вероятности ( /, и Р суммы нормальных распределений.| Графический способ разбивки произвольного закона распределения на нормальные составляющие. [22]

Каждое из распределений /) () характеризуется своим средним значением тх. Треугольное распределение, как известно, довольно точно может быть заменено нормальным законом с равной дисперсией. [23]

В качестве примера рассмотрим случай симметричного треугольного распределения спроса, при котором функция плотности распределения получается в виде графика, представленного на рис 25.1 А. [24]

Если в молекуле имеется два набора заполненных валентных орбиталей, эти наборы располагаются так, чтобы быть по возможности дальше друг от друга, и образующаяся в этом случае молекула линейна. При трех наборах валентных электронов получается плоское треугольное распределение, при четырех наборах - тетраэдрическая связь, пять наборов приводят к тригональнои бипирамиде, шесть наборов - к октаэдрическому типу связи. Образование каждой из этих геометрических фигур обусловлено тем, что наборы валентных электронов располагаются как можно дальше друг от друга. [25]

Форма МДС обмоток в зависимости от исполнения обмоток. [26]

В многофазных обмотках ягоря машин постоянного тока получается треугольное распределение МДС. [27]

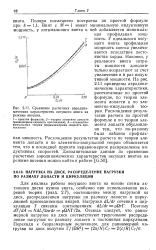Сравнение расчетных аэродинамических характеристик несущего винта на режиме висения. [28]

Для анализа работы несущего винта на основе схемы активного диска нужно знать, особенно при использовании вихревой теории ( разд. Отсюда следует, что равномерной нагрузке на диск соответствуют треугольное распределение нагрузки по размаху лопасти и постоянная циркуляция. [29]

Отметим, что треугольное распределение является сильной идеализацией и его невозможно реализовать. Расчеты, проведенные с рядом других распределений, показывают, однако, их некритичность, если они сохраняют основные особенности треугольного распределения: слабое поле на начальном участке и сильное поле в области энергообмена, где в результате квадратичной группировки формируются плотные фазовые сгустки. I) 2 ], которое достаточно близко к реальным распределениям поля в открытых резонаторах. [30]

Страницы: 1 2 3