Треугольное распределение

Cтраница 3

Описывается симметричное относительно точки 0 распределение единицы массы на отрезке [ а, 6 ], уплотняющееся к середине. Название объясняется видом графика плотности. Треугольное распределение называется также распределением Симпсона. [31]

С позиции теории рекомендуется использовать тот вид распределения, который лучше отражает фактическое положение. В большинстве случаев истинное распреде леиие вероятностей неизвестно. Эта ситуация описывается с помощью треугольного распределения. [32]

Предположения, которые были высказаны указанными авторами о закономерностях распределения ошибок измерения, были весьма различны. Симпсон исходил из предположения, что малые ошибки допускаются чаще, чем большие и также ограничены по абсолютной величине некоторым числом а. Симпсон считал, что ошибки подчинены треугольному распределению, плотность которого равна 0 в отрезках от - до - а и от а до; в отрезке ( - а, 0) ее уравнение будетх - 2аг у - а и, наконец, в лтрезке ( 0, а) имеет уравнение х Id1 у а. Следует заметить, что как Коте, так и Симпсон не рассматривали в сущности плотности распределения, поскольку они считали, что ошибки укладываются в арифметическую прогрессию с очень малой разностью и неопределенным числом возможных значений. [33]

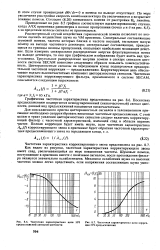
Погрешность от колебаний напряжения питания ( o / j) распределена по треугольному закону, а суммарная погрешность нуля ( 0) - по трапецеидальному. Кривой для суммирования таких распределений на рис. 3 - 2 нет. Однако на рис. 3 - 3 есть кривая 2 для суммирования треугольного распределения с дискретным двузначным. Воспользуемся этой кривой следующим образом. Тогда нужная нам кривая будет проходить всегда выше кривой 2 на рис. 3 - 3, но она не может быть выше кривой 6 на рис. 3 - 3, соответствующей нормальному распределению. Узкая полоса между этими кривыми в их начальной части и ограничивает возможное положение нужной нам кривой. [34]

Погрешность от колебаний напряжения питания ( ои) распределена по треугольному закону, а суммарная погрешность нуля ( ан) - по трапецеидальному. Кривой для суммирования таких распределений на рис. 3 - 2 нет. Однако на рис. 3 - 3 есть кривая 2 для суммирования треугольного распределения с дискретным двузначным. Воспользуемся этой кривой следующим образом. Будем считать исходным распределением треугольное ( аи), а добавляемым к нему - трапецеидальное ( ои) - Тогда нужная нам кривая будет проходить всегда выше кривой 2 иа рис. 3 - 3, но она не может быть выше кривой 6 на рис. 3 - 3, соответствующей нормальному распределению. Узкая полоса между этими кривыми в их начальной части и ограничивает возможное положение нужной нам кривой. [35]

Частотная характеристика цепи НЧ предыскажсний сигналов цветности.| Частотная характеристика цепи коррек-ции НЧ предыскажений. [36]

Рассмотренный случай воздействия гармонической помехи позволяет по аналогии оценить воздействие шума на ЧМ приемник. Спектральные составляющие шумовой помехи, частота которых близка к частоте несущей, вызывают малую помеху на выходе частотного детектора; спектральные составляющие, приходящиеся на границы полосы пропускания, оказывают наибольшее мешающее действие. Треугольное распределение энергии помехи в спектре сигналов цветности системы SECAM позволяет следующим образом повысить помехоустойчивость. Цветоразностные сигналы на передающем конце подвергаются предварительной частотной коррекции - предыскажениям. Корректирующая цепь обеспечивает подъем высокочастотных компонент цветоразностных сигналов. [37]

Форма МДС обмоток в зависимости от способа выполнения обмоток. [38]

Обмотки электрических машин - контуры с током, они создают в воздушном зазоре МДС. Простейшая обмотка - - катушка, состоящая из одного или нескольких витков. В многофазных обмотках якоря машин постоянного тока получается треугольное распределение МДС. [39]

Перед тем как оценить возможное число залежей, оценивается число перспективных ловушек рассматриваемой перспективной зоны. Если степень геологической и геофизической изученности достаточно велика, то все перспективные ловушки могут быть известны. Если же такие сведения отсутствуют, то для определения числа перспективных ловушек ( структур) используется показатель плотности структур, то есть числа структур, приходящихся на единицу площади по аналогичным разведанным перспективным зонам того же бассейна. Если же этот показатель оценить невозможно, при определении числа ловушек вначале оцениваются верхняя и нижняя границы возможного их числа, а вероятность промежуточных значений задается некоторым законом распределения на основе имеющейся геологической и геофизической информации. Если сведения о законе распределения числа ловушек отсутствуют, часто принимается так называемое треугольное распределение. Плотность такого распределения графически изображается треугольником. [40]

СКО связана с тем, что интервалу приходится приписывать определенное числовое значение вероятности. Часто при этом считают распределение равномерным. Это означает приравнивание нашего незнания равномерной плотности распределения. Указано, что характеристика максимальные пределы неопределенности идентифицируется как интервал, соответствующий вероятности, равной единице. Иногда принимают треугольное распределение. [41]

В случае экспериментального снятия изотермы 1 ее отличие от обычной логарифмической в области средних заполнений вполне может быть объяснено погрешностями измерения. Наиболее значительно расхождение между кривыми 1 и 2 на концах интервала. Однако следует помнить, что в этих областях обе кривые неверны. Приближенный способ вычисления изотермы, описанный выше, вблизи концов интервала неприменим. Более точное вычисление обеих изотерм позволяет поправить кривые 1 и 2 в этих областях. Исправленные кривые нанесены пунктиром в левом конце рассматриваемого интервала. Из чертежа ясно видно, что исправленные кривые проходят близко одна от другой практически во всей рассматриваемой области. Таким образом, треугольное распределение энергии адсорбции приводит к изотерме, которая мало отличается от логарифмической. На том же рисунке кривая 3 изображает изотерму адсорбции для равномерного распределения с той же шириной, что и у треугольника. [42]

Распределение скорости при телескопическом течении. [43]

Если жидкость протекает через цилиндрическую трубку, то течение может быть либо турбулентным, либо ламинарным. При турбулентном течении траектории частиц представляют собой волнообразные кривые, образующие завихрения. Турбулентное течение происходит при малых скоростях, если только трубка сравнительно широка. Следовательно, от стенки к центру имеется градиент скорости аналогично тому, как при стационарном движении пластинки на рис. I. Большинство физиков решат, что такое распределение скоростей маловероятно. Излом кривой - это то, что в математике называется особенностью; представляется весьма странным, чтобы особенность встречалась в физической задаче. Freundlich) и Шалек ( Schalek, 1924 г.), которые в одной из своих работ предполагают треугольное распределение скоростей. Далее будет показано, что нет необходимости делать какое-либо предположение о распределении скоростей, но, прежде чем сделать это, коротко опишем работу Гагена, как первую, опубликованную по вязкой жидкости. Гаген изучал течение воды в латунных трубках радиусом от 1 до 3 мм и длиной от 0 5 до 1 м, соединявших горизонтально два резервуара, в которых вода поддерживалась на разных уровнях. [44]

Страницы: 1 2 3