Другое распределение
Cтраница 1
Другое распределение, связанное с показательным. [1]
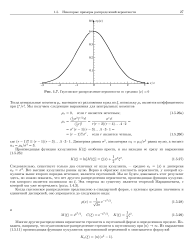 |
Гауссовское распределение вероятности со средним ( ж О. [2] |
Многие другие распределения вероятности стремятся к гауссовской форме в определенном пределе. Покажем, например, что пуассоновское распределение стремится к гауссовскому при ( п) - сю. [3]
Всякое другое распределение потенциалов на выходах вентилей В1 - Вв недействительно, поскольку приводит к расхождению с исходным состоянием основного триггера. [4]
Использование других распределений вносит в методику испытаний усложнения; однако, чтобы получить из испытаний правильные выводы, необходимо решать возникающие при этом задачи ( см. гл. [5]
Для других распределений способы приближенного преобразования случайных чисел на ЭВМ иные. [6]
Для других распределений внешней скорости в общем случае получаются бесконечные ряды, члены которых, как правило, быстро уменьшаются, и в большинстве практических случаев ряд быстро сходится. В качестве примера следовало бы привести отрицательную степень ( возрастание давления) / п - 0 09 или р - 0 199, что имеет место непосредственно у границы отрыва потока. [7]
При других распределениях плотности вероятностей погрешность зависит от вероятности. [8]
Возможны и другие распределения переменных на зависимые и независимые, : хотя в практике расчетов они встречаются нечасто. Например, , предлагаемые алгоритмы могут быть использованы для рас - чета констант фазового равновесия, требуемых при расчете однократного испарения. Одним словом, исходя из конкретной постановки задачи, исследователь должен сам выбрать ту или иную методику расчета. [9]
Возможны и другие распределения. Такие распределения называются пространственными, причем подразумевается не обычное, а фазовое пространство. [10]
Для всякого другого распределения усилий распределение напряжений на концах стержня будет отличаться от того, которое дает решение ( 59), однако в силу принципа Сен-Венана на большом расстоянии от концов решение остается справедливым. [11]
Для всякого другого распределения усилий распределение напряжений на концах стержня будет отличаться от того, которое дает решение ( 59), однако в силу принципа Сен-Венана на большом расстоянии от концов решение остается справедливым. [12]
Возможны также многие другие распределения, кроме устанавливаемых теоремой 9, но еще не найдены простые критерии для их описания. [13]
Зельдович, приняв другое распределение для адсорбционных мест, вывел также для средних заполнений ранее найденное эмпирически уравнение Фрейндлиха: Г йс1 / п, где k и п - постоянные. [14]
Могут использоваться и другие распределения. [15]
Страницы: 1 2 3