Другое распределение

Cтраница 3

Аналогичный критерий, но с другим распределением может быть применен к отклонениям от равновесия, возникающим в регрессионной модели, включающей только коинтегрированный набор переменных. [31]

Чтобы использовать символическую программу при другом распределении памяти, достаточно заново произвести ее кодировку - сама же символическая программа остается без изменения. Поскольку символическая программа не зависит от распределения памяти, то в нее легко вносить изменения. [32]

Для твердого состояния должно быть использовало другое распределение по ориентациям. При этом при отыскании средпей вероятности перехода нужно опять вести интегрирование типа ( 28), но в котором экспоненциальную функцию распределения нужно заменить на другую функцию. Обычно считают, что в твердых растворах ( приготовляемых в отсутствие поля) распределение все равно остается изотропным даже при наложении внешнего поля. [33]

Для твердого состояния должно быть использовано другое распределение по ориентациям. При этом при отыскании средней вероятности перехода нужно опять вести интегрирование типа ( 28), но в котором экспоненциальную функцию распределения нужно заменить на другую функцию. Обычно считают, что в твердых растворах ( приготовляемых в отсутствие доля) распределение все равно остается изотропным даже при наложении внешнего поля. [34]

Отметим, что Я. Б. Зельдович, приняв другое распределение для адсорбционных мест, вывел также для средних заполнений ранее найденное эмпирически уравнение Фрейндлиха: Г - КС1 /, где / Сип - постоянные. [35]

Важную роль в статистике играют и другие распределения вероятностей. Среди них можно, в частности, назвать 1) / - распределение Стьюдента, полезное в статистических выводах и при вычислении доверительных интервалов для истинных средних значений; 2) F-распределение, которое используется при проверке на равенство пар средних квадратов. [36]

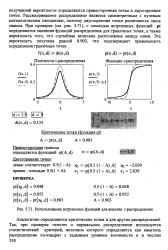Использование встроенных функций для анализа г-распределения. [37]

Аналогично определяются критические точки и для других распределений. [38]

При другом выбранном значении EJ - получается другое распределение плотности состояний. Если кривые для различных EJ - можно совместить подбором множителя Njff ( E) - l, то полученная величина N tf ( E) будет представлять эффективную плотность конечных состояний и, таким образом, будет найдена также плотность состояний валентной зоны. Если указанную процедуру можно проделать, подтверждается применимость модели непрямых переходов дли описания фотоэмиссионных процессов. [39]

Это распределение можно рассматривать как предельное для других распределений, когда стандартное отклонение стремится к нулю. [40]

Отметим, что правило Хунда не запрещает другого распределения электронов в пределах подуровня. [41]

Доказана необходимость равномерного, а не какого-либо другого распределения начальных микросостояний для получения флюктуационной формулы ( стр. [42]

Видимо, это выражение подходит и для другого распределения аэрозольных частиц по зарядам. [43]

Страницы: 1 2 3