Пуассоновское распределение

Cтраница 2

Можно ли получить точное пуассоновское распределение для больших ц, выработав соответствующую нормальную случайную величину и преобразовав ее каким-нибудь удобным способом в целое число, пользуясь при этом ( возможно усложненной) поправкой на небольшой процент времени. [16]

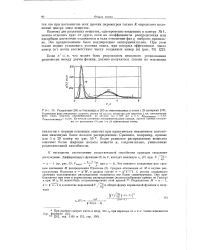
Сравнение экспериментальной и теоретической функций распределения / ( 4 для сферических областей радиуса г, содержащих четыре галактики ( Saslaw and Hamilton, 1984. [17]

Моделирование начинается с пуассоновского распределения галактик одинаковой массы, движение которых определяется одним только хабблов-ским расширением. [18]

Таким образом, нормальное и пуассоновское распределения могут выступать в качестве предельных в схеме серий. [19]

Таким образом, нормальное и пуассоновское распределения могут выступать в качесчве предельных в схеме серий. Если ТП - - Т, то интуитивно понятно, что, поскольку Т есть сумма независимых одинаково распределенных случайных величин, то предельная величина Т должна быть также суммой независимых одинаково распределенных случайных величин. [20]

В свою очередь, пуассоновское распределение переходит в нормальное. Можно показать, что биномиальное распределение переходит непосредственно в нормальное распределение. [21]

Условимся считать, что пуассоновское распределение с нулевым параметром имеет случайная величина, тождественно равная нулю. [22]

Итак, Nt имеет пуассоновское распределение с параметром А. [23]

Разделение 200 мг бензамида и 200 мг никотинамида в лотке с 29 камерами. Подвижная фаза этилацетат. скорость потока 60 мл / час. отверстие для перетока 2 мм. неподвижная фаза вода. скорость перемешивания 25 об / мин. vm 580 мл. р 1. - Кдензамида 3 59. никотинамида По точкам построена экспериментальная кривая, другие кривые построены по уравнению ( 3 для 5 и 29 эффективных камер. [24]

С ростом ожидаемого значения пуассоновское распределение становится все более симметричным. [25]

Самая простая модель - однородное пуассоновское распределение - часто используется для сравнения. Взятое в качестве исходного состояния, которое затем испытывает динамическую эволюцию, оно позволяет получить хотя бы первоначальную информацию. В качестве эталона при сравнении с наблюдаемой картиной это распределение дает меру глобальной неоднородности. Разделим, например, участок небесной сферы, где наблюдается распределение галактик до определенной звездной величины, на т равновеликих площадок. [26]

Известно далее, что нормированное пуассоновское распределение при парамет ре, стремящемся к бесконечности, сходится к нормальному распределению. [27]

Рассмотрим, например, начальное пуассоновское распределение по уровням. [28]

Таким образом, параметры пуассоновского распределения индивидуальны для многокомпонентных смесей и могут применяться для исследования и идентификации нефтей яефвепродуетов полимеров с аи-ким ИМР к других смесей природного а техничеокоиз ния. [29]

Таким образом, параметры пуассоновского распределения индивидуальны для многокомпонентных смесей z могут применяться для исследования и идентификация нефтей. [30]

Страницы: 1 2 3 4