Пуассоновское распределение

Cтраница 3

В частности, дисперсия пуассоновского распределения совпадает со ср. [31]

С более общим случаем составного пуассоновского распределения приходится сталкиваться, когда переменная г является суммой N случайных наблюдений ni9 распределенных по некоторому за -, кону, а N - пуассоновская переменная со средним Kt. [32]

Но оказывается, что это пуассоновское распределение не дает всех столкновений. И эта формула Смолуховского тоже не дает всех возможных двойных столкновений. Смолуховский рассчитал частоту столкновений при условии, что стокновение обязательно, с вероятностью 1, дает продукт реакции. В действительности же, в результате столкновения реакция может и не произойти. Поэтому возможны повторные столкновения одной и той же пары партнеров. [33]

Подобно распределению Бернулли, ширина пуассоновского распределения увеличивается с ростом ( п), но относительная ширина постепенно падает при ( п) - сю. [34]

Заметим, что параметр т пуассоновского распределения ( 69) до сих пор определен не был. [35]

В соответствии с этим допущение пуассоновского распределения активных дефектов предполагает, что последующее увеличение числа поверхностей раздела во всем образце не уменьшает общего числа дефектов. [36]

В асимптотических перечислениях часто появляются нормальное и пуассоновское распределения. Возможно, это происходит оттого, что многие комбинаторные проблемы связаны с асимптотической независимостью некоторого типа. Вероятностные аспекты наиболее отчетливо проявляются в задачах размещения шаров по ячейкам, которым посвящена уже довольно большая литература. Статья Харриса и Парка [24] иллюстрирует получаемые в этом направлении результаты и содержит ссылки на более ранние работы. [37]

Рассмотрим теперь случай сводимости к пуассоновскому распределению. [38]

Ключевые слова: оптические спектры, пуассоновское распределение, рвятгеноструктурный анализ, константы скорости, энергии орбиталей, ассоциация, - тГ - комплексы. [39]

Хп и Yn независимы и имеют пуассоновские распределения с параметрами [ Хп ] и Я. [40]

Эта аргументация выглядит как новый вывод пуассоновского распределения, но на самом деле это только перефразировка первоначального вывода из 1, гл. [41]

Погожев заинтересовался вопросом быстроты сближения с пуассоновским распределением, в зависимости от числа слагаемых потоков. Хинчина-Ососкова методы классической теории суммирования. Им найдены необходимые и достаточные условия сближения суммарного потока с нестационарным пуассоновским; эти условия особенно просты в том случае, когда суммируются потоки типа процессов восстановления. Им же рассмотрен во всей полноте вопрос асимптотического разложения. [42]

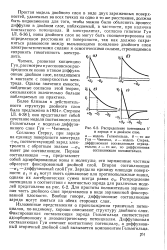Распределение потенциала V. [43]

Чэпмен, развивая концепцию Гун, рассмотрел пуассоновское распределение ионов в таком диффузионном двойном слое, находящемся в контакте с поверхностью электрода. Однако значения емкости, найденные согласно этой теории, оказываются значительно больше наблюдаемых на практике. [44]

Исключение составляет теория Кубо [785], предполагающая пуассоновское распределение расстояний между уровнями. При понижении температуры эта теория предсказывает как увеличение Хнечет по закону Кюри, так и менее выраженный рост Хчет До предельного значения % чет го 1 6 ХР, где ХР - парамагнитная восприимчивость Паули. [45]

Страницы: 1 2 3 4