Распространение - скачок
Cтраница 3
 |
Конфигурации точного решения задачи Римана о распаде произвольного гидродинамического разрыва. [31] |
Решение состоит из двух гидравлических скачков, или двух волн Римана, или гидравлического скачка и волны Римана, разделенных тангенциальным разрывом. При этом все перечисленные элементарные решения отделены друг от друга областями с постоянными значениями параметров. Чтобы полностью решить задачу Римана для течения, представленного на рис. 4.4 е, достаточно определить и и h в центральной зоне, знать скорости распространения скачков, тангенциальной поверхности и волн Римана, а также характеристики потока жидкости внутри веера волн Римана. [32]
В работе [44] предложена методика расчета режимов сложной газотранспортной системы для всего диапазона стационарных или неустановившихся изотермических или неизотермических режимов транспорта газа. Эти расчеты проводятся в целях оперативного управления газопроводами для определения фактических параметров газопроводов, оценки времени установления переходного режима эксплуатации газотранспортной системы; получения характеристик типовых режимов эксплуатации газопроводов в целях использования их для принятия тех или иных решений в различных технологических ситуациях; предотвращения и уменьшения последствий аварийных ситуаций; выбора пусковых реж: имов газопроводов; экономичного режима эксплуатации систем магистрального транспорта газа. Тем не менее, для оценки специфических режимов течения газа ( например, в аварийных ситуациях) нужны такие математические модели, которые с достаточной точностью описывали бы следующие процессы: внезапную остановку перекачки газа ( т.е. перекрытие газопровода) в двух различных сечениях, перекрытие газопровода в одном сечении, распространение скачка давления и температуры по длине газопровода и др. Необходимость разработки указанных математических моделей обусловлена возможностью количественной и качественной оценки предлагаемых конструктивных решений газопровода. [33]
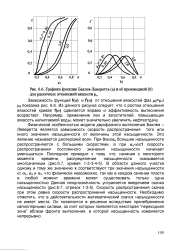 |
Графики функции Баклея-Леверетга ( а и ее производной ( Ь для различных отношений вязкости ц. [34] |
Физической особенностью модели двухфазного вытеснения Баклея - Леверетта является зависимость скорости распространения того или иного значения насыщенности от величины этой насыщенности. Это явление называется дисперсией волн. При 0aan большие насыщенности распространяются с большими скоростями, а при апст1 скорость распространения постоянного значения насыщенности начинает уменьшаться. Скорость распространения скачка при этом равна скорости распространения насыщенности. Необходимо отметить, что в действительности математический скачок насыщенности не имеет места. Он появляется в решении вследствие пренебрежения капиллярными силами, за счет которых появляется некоторая переходная зона вблизи фронта вытеснения, в которой насыщенность изменяется непрерывно. [35]
Страницы: 1 2 3