Обратное распространение

Cтраница 3

Коррекция весов, равная сумме, вычисленной алгоритмом обратного распространения, и случайный шаг, задаваемый алгоритмом Коши, приводят к системе, которая сходится и находит глобальный минимум быстрее, чем система, обучаемая каждым из методов в отдельности. Простая эвристика используется для избежания паралича сети, который может иметь место как при обратном распространении, так и при обучении по методу Коши. [31]

В работе [7] описан метод ускорения обучения для алгоритма обратного распространения, увеличивающий также устойчивость процесса. Этот метод, названный импульсом, заключается в добавлении к коррекции веса члена, пропорционального величине предыдущего изменения веса. Как только происходит коррекция, она запоминается и служит для модификации всех последующих коррекций. [32]

В [9] описан привлекательный метод улучшения характеристик обучения сетей обратного распространения. В работе указывается, что общепринятый от 0 до 1 динамический диапазон входов и выходов скрытых нейронов неоптимален. Так как величина коррекции веса Awptbk пропорциональна выходному уровню нейрона, порождающего OUTpj, то нулевой уровень ведет к тому, что вес не меняется. При двоичных входных векторах половина входов в среднем будет равна нулю, и веса, с которыми они связаны, не будут обучаться. [33]

Парадигма Delta Bar Delta является попыткой ускорить процесс конвергенции алгоритма обратного распространения за счет использования дополнительной информации об изменении параметров и весов во время обучения. [34]

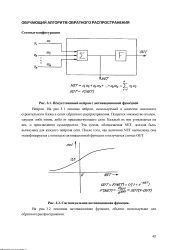Искусственный нейрон с активационнной функцией. [35]

На рис. 3.2 показана активационная функция, обычно используемая для обратного распространения. [36]

Таким образом, полный алгоритм обучения нейронной сети с помощью процедуры обратного распространения строится следующим образом. [37]

Многими исследователями были предложены улучшения и обобщения описанного выше основного алгоритма обратного распространения. Литература в этой области слишком обширна, чтобы ее можно было здесь охватить. [38]

Это улучшение было достигнуто с помощью комбинации обычных алгоритмов с сетью обратного распространения, обеспечивающей дополнительную проверку. [39]

Реализована только многослойная нейронная сеть, обучаемая с помощью модифицированного алгоритма обратного распространения. Нейропакет позволяет работать с динамическими функциями времени, поступающими в качестве входных сигналов. Оценка обусловлена тем, что многослойная нейронная сеть представляет собой половину всех используемых нейронных парадигм. [40]

На рис. 3.3 изображена многослойная сеть, которая может обучаться с помощью процедуры обратного распространения. Для ясности рисунок упрощен. Первый слой нейронов ( соединенный с входами) служит лишь в качестве распределительных точек, суммирования входов здесь не производится. Входной сигнал просто проходит через них к весам на их выходах. А каждый нейрон последующих слоев выдает сигналы NET и OUT, как описано выше. [41]

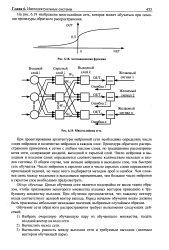Активационная функция. [42]

На рис. 6.19 изображена многослойная сеть, которая может обучаться при помощи процедуры обратного распространения. [43]

На рис. 3.1 показан нейрон, используемый в качестве основного строительного блока в сетях обратного распространения. Подается множество входов, идущих либо извне, либо от предшествующего слоя. Каждый из них умножается на вес, и произведения суммируются. Эта сумма, обозначаемая NET, должна быть вычислена для каждого нейрона сети. [44]

Даже после того как сеть обучена, невозможно сказать, найден ли с помощью обратного распространения глобальный минимум. Если решение неудовлетворительно, приходится давать весам новые начальные случайные значения и повторно обучать сеть без гарантии, что обучение закончится на этой попытке или что глобальный минимум вообще будет когда либо найден. [45]

Страницы: 1 2 3 4