Прямое распространение

Cтраница 2

Этот специальный класс сетей, называемых сетями без обратных связей или сетями прямого распространения, представляет интерес и широко используется. Сети более общего вида, имеющие соединения от выходов к входам, называются сетями с обратными связями. У сетей без обратных связей нет памяти, их выход полностью определяется текущими входами и значениями весов. В некоторых конфигурациях сетей с обратными связями предыдущие значения выходов возвращаются на входы; выход, следовательно, определяется как текущим входом, так и предыдущими выходами. По этой причине сети с обратными связями могут обладать свойствами, сходными с кратковременной человеческой памятью, сетевые выходы частично зависят от предыдущих входов. [16]

Теория кратных рядов Фурье (1.6) обширна, но в основном она состоит из прямого распространения результатов с одной переменной. Интересны, конечно, только такие результаты, которые не имеют аналогов для одного переменного или доказательство которых требует существенно новых идей. В этой главе мы ограничим наше внимание весьма частным вопросом, именно прямоугольной суммируемостью рядов Фурье ( см. ниже) и ее применениями, а в этом параграфе мы соберем несколько простых фактов и определений. [17]

Итеративная структура нейронной сети рекурсивной редукции с обратными связями может быть преобразована в структуру прямого распространения. [18]

Когда же емкость полностью заполнена жидкостью, то гидростатическое давление препятствует этому и способствует прямому распространению напряжений в места угловых соединений. [19]

В главе VII было показано, что эта аналогия не является полной, так что прямое распространение закономерностей теплообмена между газом и частицами на процесс массообмена не является правомерным. В связи с этим ниже кратко рассмотрены попытки обобщения опытных данных, полученных только в результате непосредственного эксперимента по массообмену. [20]

Для достижения высокой производительности конвейерной обработки необходимо, чтобы обратные связи рекурсивной редукции конечного кольца были заменены операциями прямого распространения. [21]

Структура сети Кохонена. [22]

На входы сети подается входной образ, и сигналы возбуждения распространяются по всем слоям согласно принципам классических сетей прямого распространения ( feedforward), т.е. для каждого нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется активационная ( передаточная) функция нейрона, в результате чего получается его выходное значение. [23]

Архитектура преобразователя СОК в двоичный код. [24]

Рассмотрим на основе модели НСКК, предложенной в предыдущем параграфе, архитектуры модулярной редукции, итерации переноса из старшего разряда и прямого распространения. [25]

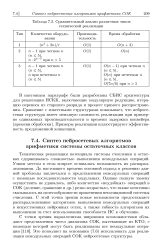Сравнительный анализ различных типов. [26]

В настоящем параграфе были разработаны СБИС архитектуры для реализации НСКК, включающие модулярную редукцию, итерацию переноса из старшего разряда и процесс прямого распространения. Примеры реализации иллюстрируют эффективность предложенной концепции. [27]

Отсюда следует, что наибольшее значение коэффициент взаимной корреляции RZI ( т) достигает при задержке времени т TO, равной времени прямого распространения звука от машины в точку наблюдения. [28]

Результаты численного расчета турбулентного уширения сфокусированного пучка при распространении сверху вниз приведены на рис. 4.5. Здесь же для сравнения приведена кривая 7, соответствующая прямому распространению. Как видно из рисунка, турбулентное расширение лазерного пучка на наклонных трассах при обратном распространении ( сверху вниз) оказывается меньше, чем при прямом. В этой же работе было показано, что он не противоречит теореме взаимности. [29]

Поскольку обсуждаемая нами структура представляет собой многослойную сеть и, как уже отмечалось, алгоритм обратного распространения ошибки можно обобщить на любую сеть с прямым распространением сигнала, то ничто не препятствует тому, чтобы предлагаемый модуль нечеткого управления обучать также, как и обычную нейронную сеть. [30]

Страницы: 1 2 3 4 5