Знак - левая часть
Cтраница 1
Знак левой части зависит от направления диффузионного потока. [1]
Рассмотрим знак левой части ( 1) в каждой из этих областей. [2]
Определяем знак левой части неравенства на каждом интервале. Исследуем сами критические точки: точка х 2 является нулем числителя и, так как неравенство нестрогое, входит в множество решений. [3]
Определяем знак левой части неравенства на каждом интервале. [4]
Определим знак левой части неравенства в каждом интервале. [5]
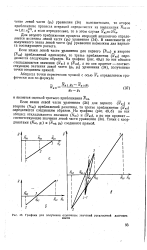 |
Графики для получения оценочных значений усталостной долговечности. [6] |
Если знаки левой части уравнения ( 34) для первого ( JVH i) и второго ( Л / н2) приближений различны, то третье приближение ( Л нз) определяется следующим образом. [7]
Следовательно, знак левой части совпадает со знаком / ( с), что означает, что (11.5) справедливо. [8]
Чтобы определить знак левой части на всем интервале, достаточно определить ее знак в одной какой-либо точке этого интервала и тем самым установить, входит ли этот интервал в множество решений данного неравенства. [9]
Будем поэтому рассматривать знак левой части на отрезке [ 0 4тг ]: его длина равна 4тг, а это число служит периодом как числителя, так и знаменателя. [10]
Как видно из ( 45), знак левой части при движении по линии aj 1 может меняться. [11]
Это следует непосредственно из того, что знак левой части уравнения ( 182) при заданном ш, отличном от ( 184), и р достаточно близком к нулю определяется знаком первого слагаемого. [12]
Это следует непосредственно из того, что знак левой части уравнения ( 182) при заданном ш, отличном от ( 184) и р достаточно близком к нулю, определяется знаком первого слагаемого. [13]
Для противотока, как уже было отмечено, знак левой части одного из основных уравнений ( 7 - 12) изменяется на противоположный. [14]
Для противотока, как уже было отмечено, знак левой части одного из основных уравнений ( 7 - 12) изменяется на противоположный. [15]
Страницы: 1 2