Рассмотрение - столкновение
Cтраница 2
Та же задача с использованием выражения (20.15) была решена также Браутом [456], причем при рассмотрении столкновения молекул для каждой из них вводился свой угол & ( см. рис. 72); члены с cos2d выражались через сферические функции, что позволило значительно упростить вычисления. [16]
Но при вычислении S4 ( о) можно было бы с таким же успехом исходить из рассмотрения столкновений, которые происходят за время dt в do между молекулой т и молекулой т1 таким образом, что до столкновения переменные лежат в пределах ( 108) и ( 109), и которые мы снова обозначим как обратные столкновения. [17]
Как уже указывалось в части I, классическая формула распределения Максвелла - Больцмана может быть выведена из рассмотрения столкновений между частицами газа. Сущность вывода заключается в следующем. Число подобных столкновений в единицу времени пропорционально произведению / / 2, где / г и / 2 - значения плотности распределения для рассматриваемых состояний. Число подобных столкновений в единицу времени пропорционально произведению / 3А - Можно показать, что коэффициент пропорциональности имеет в обоих случаях одно и то же значение. При наличии статистического равновесия среднее число частиц в каждом состоянии должно оставаться неизменным во времени, причем противоположно направленные процессы ( в данном случае прямые и обратные столкновения) должны попарно компенсировать друг друга. Это соответствует так называемому принципу детального равновесия. [18]
Для получения конечного поглощения звука в идеальном монокристалле рассматриваемого нами типа, как и в случае теплопроводности, обратимся к рассмотрению столкновения с участием четырех фононов. [19]
Интегралы У ( Р), / () были вычислены численно, причем в этих вычислениях были использованы значения /, /, соответствующие рассмотрению столкновений в неподвижной системе координат. [20]
Обратимся теперь к подробному рассмотрению того, что происходит в процессе реакции с индивидуальными молекулами реагентов А и В. Рассмотрением столкновений молекул при реакциях занимается теория столкновений, которая позволяет разобраться в механизме протекания химических реакций. [21]
Основное предположение кинетической теории газов состоит в том, что физические свойства газа существенно зависят от движения молекул и не зависят от их внутренней структуры. Поэтому при рассмотрении столкновений молекул не учитываются явления, связанные с внутренней структурой молекул, что позволяет создать простые математические модели молекул, которые очень сильно облегчают задачу определения макроскопических характеристик газа, исходя из движения молекул. Соответствие свойств газа, рассчитанных теоретически, свойствам, наблюдаемым в эксперименте, является критерием правильности исходной модели молекулы. [22]
Эта формула выведена в предположении, что все молекулы, кроме одной, покоятся. В действительности при рассмотрении столкновений молекул в газе сделанное допущение несправедливо, вследствие чего в формулу (3.4) нужно ввести поправку, учитывающую изменение вероятности столкновений из-за движения мишеней. [23]
Еще один пример приложения того же принципа можно обнаружить, рассматривая любые столкновения быстрых нуклонов с ядрами, при которых происходит разрушение ядра и образуются новые частицы. Однако оказывается, что фактически даже рассмотрение последующих столкновений возможно только при достаточно больших углах разлета частиц и энергиях отдачи нуклонов. [24]
Высказывалось предположение, что, море, соответствующее дырке в распределении партонов, само является дыркой. Это не противоречит тому, что мы предполагаем в следующей гипотезе В2 и что используется при рассмотрении адронных столкновений. Само, по себе, однако, это предположение не представляется мне разумным, если, согласно Б2, адроны образуют универсальное море. Гипотеза Б2 означает, по-видимому, что если бы существовало два сгустка адронов с разрывом между ними, то они образовали бы море партонов. Поэтому, раз нет моря партонов, нет и разделения адронных сгустков, а должно иметься море адронов. Во всяком случае, я убежден в том, что в рассматриваемой ситуации оно действительно существует и дырки в распределении по импульсам адронов, которая соответствовала бы разрыву в импульсах партонов, нет. [25]
В Actes de Leipzig для объяснения преломления света он намеревался обратиться к Философии конечных причин, которые были изгнаны Декартом, и восстановить объяснение, выведенное Декартом из рассмотрения столкновения тел, в противоположность мнению Ферма. Он начинает, следовательно, с отрицания того, что Природа действует или по наиболее короткому пути или по пути наименьшего времени; но утверждает, что она выбирает наиболее легкий путь, который не должен совпадать ни с каким из двух названных. Для определения этого наиболее легкого пути служит сопротивление, оказываемое лучу света при пересечении рассматриваемых прозрачных сред; и он предполагает, что это сопротивление различно в различных средах. Он устанавливает ( что совпадает с мнением Ферма), что в более плотных средах, таких, как вода и стекло, сопротивление больше, чем в воздухе и других разреженных средах. Допустив это, он рассматривает трудность, встречающуюся лучу при пересечении какой-либо среды, и определяет эту трудность с помощью произведения пути на сопротивление. Он утверждает, что луч всегда следует по тому пути, для которого сумма таким образом измеренных трудностей является наименьшей; и по методу максимума и минимума он находит правило, известное из опыта. Но хотя это объяснение на первый взгляд кажется согласующимся с объяснением Ферма, оно, однако, затем истолковывается с такой удивительной хитростью, что становится диаметрально противоположным последнему, и согласуется с объяснением Декарта. Ибо, хотя Лейбниц допустил, что сопротивление стекла больше, чем сопротивление воздуха, он утверждает, что луч движется в стекле быстрее, чем в воздухе; и благодаря тому, что при этом сопротивление стекла считается большим, получается, конечно, из ряда вон выходящий парадокс. [26]
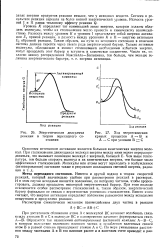 |
Энергетическая диаграмма реакции в теории переходного состояния. [27] |
Имеется и другой подход к теории скоростей реакций, который значительно удобнее при рассмотрении реакций в растворах. И в этом случае исходным является положение, по которому частицы, чтобы прореагировать, должны преодолеть некоторый энергетический барьер. При этом подходе исключается особое рассмотрение столкновений и, таким образом, энергетический барьер формально не связан с вероятностью успешного столкновения. Вместо этого считают, что энергия активации определяет положение равновесия между исходными веществами и продуктами реакции. [28]
 |
Изменение энергии в ходе экзотермической реакции. [29] |
Имеется и другой подход к теории скоростей реакций, который значительно удобнее при рассмотрении реакций в растворах. И в этом случае исходным является положение, что частицы должны преодолеть некоторый энергетический барьер для того, чтобы прореагировать. При этом подходе исключается особое рассмотрение столкновений и таким образом, энергетический барьер формально не связан с вероятностью успешного столкновения. Вместо этого считают, что энергия активации определяет положение равновесия между исходными веществами и продуктами реакции. [30]
Страницы: 1 2 3