Рассмотрение - деформация
Cтраница 2
При рассмотрении деформации осевой линии стержня в некоторый начальный момент времени все три системы координат могут совпадать, а в последующие моменты времени за счет смещения и деформации осевой линии они будут смещены относительно друг друга в пространстве. Обозначенная нами кривая L, положение точек которой в системе отсчета определяет радиус-вектор г, соответствует осевой линии стержня после ее деформации. Поэтому сопутствующая система координат имеет естественные оси. Эти векторы являются ортами сопутствующей подвижной лагранжевой системы координат. [16]
При рассмотрении деформаций элемента кривого стержня длиной ds мы исходили из предположения о том, что деформация этого элемента происходит так же, как в прямом стержне. Решим эту задачу более точно. [17]
При рассмотрении деформации осевой линии стержня в некоторый начальный момент времени все три системы координат могут совпадать, а в последующие моменты времени за счет смещения и деформации осевой линии они будут смещены относительно друг друга в пространстве. Обозначенная нами кривая L, положение точек которой в системе отсчета определяет радиус-вектор г, соответствует осевой линии стержня после ее деформации. Поэтому сопутствующая система координат имеет естественные оси. Эти векторы являются ортами сопутствующей подвижной лагранжевой системы координат. [18]
Джейл проводит морфологическое рассмотрение деформации и разрушения кристаллических полимеров. Джеллинек анализирует общую роль химических изменений в разрушении, а А. Чарлзби описывает специфическое влияние радиации на этот процесс. [19]
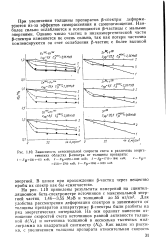 |
Зависимость относительной скорости счета в различных энергетических областях р-спектра от толщины препарата. [20] |
Для удобства рассмотрения деформации спектров в зависимости or толщины препаратов аппаратурные р-спектры были разбиты на ряд энергетических интервалов. [21]
Однако при рассмотрении деформации срединной поверхности сохранены члены до второго порядка в выражении для деформаций и до третьего порядка в выражении для энергии. Благодаря этому получено самое простое видоизменение линейной теории, позволяющее учесть взаимодействие окружных усилий с изгибом. Кроме того, сохранен дополнительный член четвертого порядка в выражении для энергии, чтобы связанные уравнения оставались ограничен-ным. В выражения для деформации и энергии введены также нелинейные члены, соответствующие начальным несовершенствам. [22]
 |
Задержка белков на ц.м. и ультрафильтрация плазмы. а, в - плазма. 6 - диали-зирующий раствор.| Ультрафильтрация диализирующего раствора, р 0 3 ати. [23] |
Перейдем теперь к рассмотрению деформации ц.м. Этот вопрос имеет существенное значение для оценки не только ультрафильтрации, но и эффективности применения высоких р, а также для выяснения прочности используемых мембран. [24]
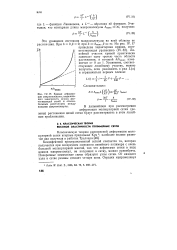 |
Кривая деформации макромолекулы, выражающая зависимость между растягивающей силой и относительным расстоянием между концами макромолекулы. [25] |
В дальнейшем при рассмотрении деформации молекулярной сетки ( резины) растяжения цепей сетки будут рассматривать в этом линейном приближении. [26]
В дальнейшем при рассмотрении деформации молекулярной сетки ( резины) растяжения цепей сетки будут рассматриваться в этом линейном приближении. [27]
Стрэтфорда основывается на рассмотрении деформации известного профиля скорости Блазиуса вниз по течению. Поэтому, строго говоря, метод не применим к потокам с отрывом впереди пограничного слоя. Стрэтфорд отметил, что в таких потоках распределение скорости при минимальном давлении с достаточной точностью может рассматриваться подобным распределению скорости Блазиуса в соответственно выбранном масштабе. [28]
Выше отмечалось, что рассмотрение деформаций, близких к изгибаниям срединной поверхности, предъявляет повышенные требования к исходной системе уравнений. [29]
Второе уравнение составляется из рассмотрения деформации бруса. [30]
Страницы: 1 2 3 4