Рассмотрим - графа
Cтраница 1
Рассмотрим граф, соответствующий этой межотраслевой модели. Введем вершину общего потребления С и зададим поток ( потребление) из этой вершины в каждую отрасль. Величина этого потока равна чистому выпуску отрасли и находится как сумма элементов соответствующей строки матрицы. [1]
Рассмотрим граф, вершины которого представляют сотрудни - - ков некоторого учреждения, а дуги - линии связи между сотрудниками. Тогда граф, представляющий только наиболее важные каналы связи данного учреждения, является остовным подграфом, граф, который подробно представляет линии связи только какойт то части этого учреждения ( например, отделения), является порожденным подграфом, а граф, который представляет только важные-линии связи в пределах отделения, является подграфом. [2]
Рассмотрим граф О - ( X, А), в котором ( XI, х) А тогда и только тогда, когда символ хг может быть спутан с символом X ] на приемном конце канала связи. [3]
Рассмотрим граф О, изображенный на рис. 5.8. Число, стоящее около любого ребра, задает его длину; вес каждой вершины графа равен единице. Требуется найти абсолютный р-центр с минимально возможной величиной параметра р и такой, чтобы каждая вершина графа отстояла хотя бы от одного из этих р центров на расстоянии, не превосходящем 3 5 единиц. [4]
Рассмотрим граф, изображенный на рис. 8.1, где каждое неориентированное ребро рассматривается как пара противоположно ориентированных дуг равного веса. [5]
Рассмотрим граф С, в котором каждой дуге ( х 1 X)) приписаны два числа ргз и, представляющие соответственно надежность и пропускную способность дуги. Задача нахождения пути от к I с наибольшей приведенной пропускной способностью является комбинацией двух последних задач о путях, обсуждавшихся выше-в разд. [6]
 |
Граф из примера. [7] |
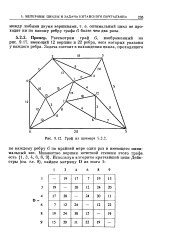
Рассмотрим граф С, изображенный на рис. 9.12, имеющий 12 вершин и 22 ребра, веса которых указаны у каждого ребра. [8]
 |
Граф из примера. [9] |
Рассмотрим граф, изображенный на рис. 11.1, и возьмем в качестве источника вершину х, а в качестве стока - вершину хд. Пропускные способности дуг указаны на рисунке. [10]
Рассмотрим граф с п8 источниками и п ( стоками и предположим, что поток может идти от любого источника к любому стоку. [11]
 |
Граф из примера Первая пометка является пропускной способностью дуги, вторая - стоимостью дуги. [12] |
Рассмотрим граф О, изображенный на рис. 11.13, где первое число пометки у каждой дуги равно ее пропускной способности, а второе - стоимости. [13]
Рассмотрим граф, вершины которого соответствуют отделениям, а ребра указывают, какие пары соседних отделений соединены проходом. [14]
 |
Граф UQ. [15] |
Страницы: 1 2 3 4 5