Рассмотрим - графа
Cтраница 3
Рассмотрим граф, изображенный на рис. 50, Пропускные способности написаны рядом с дугами Жирными линиями выделены дуги входящие в дерево путей. Путь может использоваться для потока в 2 единицы. Штрихами выделена дуга, замыкающая путь. Далее получающиеся графы приводятся без пояснений на рис. 52 - 58 На рис. 58 видно окончательное решение. Штрихами помечены дуги разреза. [31]
Рассмотрим граф, который имеет п вершин и m ребер; воспользуемся обозначениями упр. [32]
Рассмотрим граф G, представленный на рис. 2.1, а. Пунктиром на рисунке показаны удаляемые транзитивные дуги. [33]
Рассмотрим граф G, принадлежащий классу Аг. Пусть в каждой из г 2 нечетных компонент выбрано по одной вершине. [34]
Рассмотрим граф G, изображенный на рис. 5.8. Число, стоящее около любого ребра, задает его длину; вес каждой вершины графа равен единице. Требуется найти абсолютный р-центр с минимально возможной величиной параметра р и такой, чтобы каждая вершина графа отстояла хотя бы от одного из этих р центров на расстоянии, не превосходящем 3 5 единиц. [35]
Рассмотрим граф G, в котором каждой дуге ( xt, Xj) приписаны два числа ptj и qtj, представляющие соответственно надежность и пропускную способность дуги. Задача нахождения пути от s - к t с наибольшей приведенной пропускной способностью является комбинацией двух последних задач о путях, обсуждавшихся выше-в разд. [36]
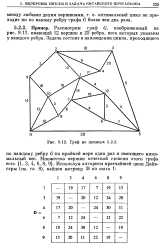 |
Граф из примера. [37] |
Рассмотрим граф G, изображенный на рис. 9.12, имеющий 12 вершин и 22 ребра, веса которых указаны у каждого ребра. [38]
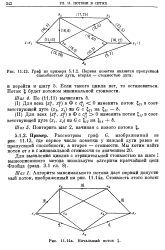 |
Граф из примера Первая пометка является пропускной способностью дуги, вторая - стоимостью дуги. [39] |
Рассмотрим граф G, изображенный на рис. 11.13, где первое число пометки у каждой дуги равно ее пропускной способности, а второе - стоимости. [40]
Рассмотрим граф G, вершинами которого являются буквы алфавита, а смежность вершин означает, что буквы могут быть перепутаны. Тогда максимальное число однобуквенных сообщений, которые можно послать, не опасаясь перепутать их, оче видно, равно a ( G) - максимальному числу независимых вершин в графе G. Ясно, что существует по крайней мере a ( Gk) таких слов ( образованных из максимального множества неперепутываемых букв), но их может быть и больше. Обозначим через a ( G) & максимальное число iWs, з 5, 4 2 и 5 4 неперепутываемы. [41]
Рассмотрим граф G ( XE) с множеством ребер E [ ] i MRt - Очевидно, что понятия Af-клики в ассоциативной схеме и независимого множества в графе G совпадают. [42]
 |
Приведение простого графа сигналов. [43] |
Рассмотрим граф сигналов, изображенный вверху на рис. 14.16. Общая передаточная функция графа есть некоторая дробь. [44]
Рассмотрим граф G (, п), каждой вершине которого взаимно однозначно соответствует элемент из множества К-значных векторов длины п, и две вершины смежны тогда и только тогда, когда соответствующие им векторы отличаются во всех разрядах. Легко показать, что граф G ( K, и) содержит К вершин и ( К ( К-1)) / 2 ребер. [45]
Страницы: 1 2 3 4 5