Приведенное рассуждение
Cтраница 2
Приведенное рассуждение справедливо не только для деформаций растяжения и сжатия, но и для любых малых деформаций. Если деформации малы, то упругие постоянные тел не изменяются при деформациях. Отсюда следует, что если на тело действует несколько сил, то для вычисления результирующей деформации можно вычислить сначала деформации, вызываемые каждой силой в отдельности ( как если бы остальных сил не было вовсе), а затем полученные деформации сложить. Это важное положение называется принципом суперпозиции малых деформаций. [16]
Приведенное рассуждение, поскольку оно основано на соображениях симметрии, не вызывает возражений, если начальное распределение деформации само обладает требуемой симметрией. Но рассуждение остается применимым и в тех случаях, когда это условие не выполняется. Чтобы убедиться в этом, достаточно мысленно разбить начальную возмущенную область на бесконечно малые области. [17]
Приведенное рассуждение позволяет прогнозировать характер фильтрационных аномалий нелинейно вязких жидкостей. Естественно, что для прогнозирования необходимо иметь реологические кривые в области скоростей сдвига ( у), наблюдаемых в пористой среде. [18]
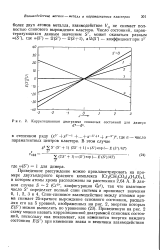 |
Корреляционная диаграмма спиновых состояний для димера. [19] |
Приведенное рассуждение можно проиллюстрировать на примере двухъядерного красного комплекса [ Сг2 ( СН3СО2) 4 ( 1 0) 2 ], в котором атомы хрома расположены на расстоянии 2 64 А. [20]
Приведенное рассуждение справедливо не только для деформаций растяжения и сжатия, но и для любых малых деформаций. Если деформации малы, то упругие постоянные тел не изменяются при деформациях. Отсюда следует, что если на тело действует несколько сил, то для вычисления результирующей деформации можно вычислить сначала деформации, вызываемые каждой силой в отдельности ( как если бы остальных сил не было вовсе), а затем полученные деформации сложить. Это важное положение называется принципом суперпозиции малых деформаций. [21]
Приведенное рассуждение, поскольку оно основано на соображениях симметрии, не вызывает возражений, если начальное распределение деформации само обладает требуемой симметрией. Но рассуждение остается применимым и в тех случаях, когда это условие не выполняется. Чтобы убедиться в этом, достаточно мысленно разбить начальную возмущенную область на бесконечно малые области. [22]
Приведенное рассуждение является чисто качественным и может привести к неверным выводам. [23]
Приведенное рассуждение основано на предположении, что три заместителя при атоме углерода, несущем неспаренный электрон, копланарны, а орбита этого электрона направлена нормально к соответствующей плоскости. [24]
Приведенное рассуждение объясняет, почему в эту формулу входит именно начальная ( а не конечная) скорость электрона. [25]
Приведенное рассуждение не зависит от того, посредством какого процесса осуществлен переход теплоты от тела А к телу В - теплопроводностью или излучением. Существенно лишь, что температуры обоих тел различны. [26]
Приведенное рассуждение принадлежит Варнингу. [27]
Приведенное рассуждение очень нестрогое. Оно не учитывает возможности уже упоминавшегося парадокса Гиффена. Этот парадокс будет проанализирован в дальнейшем с помощью порядкового подхода к анализу полезности и спроса. [28]
Приведенное рассуждение представляет собой по существу эмпирическое правило, сформулированное Краммом, которое позволяет достаточно точно предсказать стереохимию основного продукта большого числа подобного рода реакций присоединения. [29]
Приведенное рассуждение является поразительным примером силы общих соображений. Если бы основные идеи этого рассуждения принадлежали мне, то я действительно имел бы чем гордиться; но они известны уже по крайней мере в течение 60 лет. Со мной же произошло следующее. Мне пришла в голову теорема о постоянном объеме ( кстати, я впервые узнал о ней незадолго до этого) и, чтобы немного отвлечься, я переключился на небесную механику. [30]
Страницы: 1 2 3 4