Несложное рассуждение

Cтраница 1

Реологические характеристики межфазного адсорбционного слоя водного раствора лизоцима на разных углеводородных границах ( с 1 0 г / 100 мл. рН 5 3. 20 С. [1]

Несложное рассуждение показывает, что толщины адсорбционных слоев ВПАВ лежат в пределах от нескольких десятков до нзскольких тысяч ангстрем. С учетом толщины адсорбционных мэжфазных слоев проведем приближенный пересчет реологических параметров на объемные. [2]

Несложное рассуждение позволяет перейти от интегрирования степени к интегрированию произвольного степенного ряда. [3]

Несложное рассуждение показывает, что это определение совпадает с определением 4.1, когда А и х вещественны. [4]

Проведенное несложное рассуждение дает также предписание, т.е. алгоритм ( или алгорифм), для нахождения частного Ь и остатка г в конечное число шагов. [5]

Путем несложных рассуждений можно найти верхний предел наибольшей массы, который могут обеспечить сильные отталкива-тельные взаимодействия при больших плотностях. При р Ю15 г см-3 такие силы едва ли будут существенны. Тогда масса сферы, в которой уравнение состояния выполняется до р - 1015 и где давление р быстро падает при р - 0, дается нашим решением ( 22) - она имеет порядок IATIQ. Представляется правдоподобным, что найденный нами предел - 0 7tti0 близок к истине. [6]

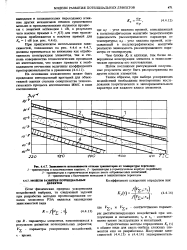Зависимость интенсивности отказов транзисторов от температуры переходов. [7]

Путем несложных рассуждений полученные результаты могут быть распространены на другие классы элементов. [8]

Сравнительно несложными рассуждениями можно показать, что если и возможен переход к ньютоновской скорости звука, то не на низких, а на очень высоких частотах. [9]

Введем несложное рассуждение, сводящее задачу отыскания оптимального плана к игровым ситуациям. [10]

Приводимое ниже несложное рассуждение показывает, каковы неулучшаемые алгоритмы в классе алгоритмов без прерывания. Рассмотрим произвольный алгоритм отбора, допускающий следующую ситуацию: в момент при длине очереди / пх очередное событие отправляется на экспресс-обработку, а в другой момент t % при меньшей длине очереди ( та С тг очередное событие отправляется на экспресс-обработку. Совершенно ясно, что число отправляемых на экспресс-обработку событий не изменилось бы, а средние потери уменьшились, если бы алгоритм управления распорядился по другому - в первом случае воздержался от направления на экспресс-обработку, а во втором - отправил событие на экспресс-обработку. [11]

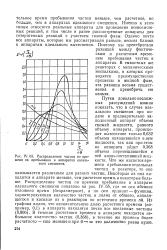Распределение частиц по времени их пребывания в аппаратах идеального смешения. [12]

Путем довольно несложных рассуждений можно показать, что в случае идеального смешения при подаче в предварительно заполненный аппарат объема свежей жидкости, равного объему аппарата, происходит вытеснение только 0 632 объема находившейся в нем жидкости, так как при этом из аппарата уйдет 0 368 объема перемешавшейся с ней вновь поступившей жидкости. [13]

После этих несложных рассуждений остается решить главный вопрос: при каком условии две возрастающие арифметические, прогрессии с общими членами ап и Ьп, причем а bi, объединенные, так сказать, в одну кучу, составят новую прогрессию. Рассмотрим эту общую задачу. [14]

С помощью несложных рассуждений можно убедиться, что построенное отображение Ре непрерывно на Q0 и переводит Q0 в себя. [15]

Страницы: 1 2 3