Знание - уравнение
Cтраница 1
Знание уравнений ( 1) отображения S1 на S2 позволяет изучить метрич. [1]
Знание уравнений основных линий, изучаемых в школьном курсе геометрии, сводится к решению двух учебных задач: а) по заданным геометрическим свойствам линии составить ее уравнение; б) по заданному уравнению линии выяснить ее геометрические свойства. В курсе алгебры вторая задача выражается иначе: по заданному уравнению построить график ( изобразить график) линии и с помощью графического языка выяснить свойства функции, а затем по возможности выясненные свойства перевести на аналитический язык. [2]
Для решения графическим методом не требуется знание уравнений геометрических образов; при аналитическом решении нет необходимости в геометрических построениях. Поэтому, если воспользоваться этими свойствами графического и аналитического методов, то можно с их помощью создать новый метод, удовлетворяющий отмеченным требованиям. [3]
Однако если для исследования путем физического моделирования требуются только знание уравнений элементов систем, только характеристика физики явления, то для математического моделирования требуется несравненно больше: нужно еще получить определенную систему уравнений, найти математические формулировки граничных условий и привести эти уравнения к удобной для решения форме. [4]
 |
График к доказательству частот -. - следовательно, уравнение систе - ного критерия. [5] |
Частотный критерий устойчивости особенно интересен тем, что не требует для-евоего применения абязательного знания уравнения системы или ее передаточной функции. Надо лишь иметь амплитудно-фазовую характеристику еистеныг которая может быть получена и экспериментально, что во многих случаях проще, точнее и надежнее. Применение же других вышеизложенных критериев требует знания дифференциального уравнения исследуемой системы автоматического регулирования. [6]
Для таких предсказаний, опирающихся на изначальные свойства атомов данного элемента, необходимо знание уравнений, специфичных не только для каждого элемента или химического соединения, но и для тех конкретных задач, которые требуется разрешить, изучая химию избранного элемента. Число таких уравнений бесконечно велико, но в силу внутреннего квантовомеханического и электронного единства Системы все они в чем-то основном могут быть между собой сходны: например, иметь единую форму и отличаться друг от друга только коэффициентами или числом слагаемых ( числом электронов), принадлежать к одному и тому же семейству уравнений, выражаемых графически кривыми или поверхностями одного и того же математического типа. [7]
Ответ на второй вопрос может быть продиктован лишь требованиями технологии и эксплуатации, и знание уравнений ( 10 - 13) не может ликвидировать расхождение в точках зрения проектировщиков, если такое расхождение имеет место. [8]
Метод преобразованного механизма отличается от предыдущего тем, что при определении ошибки этим методом не требуется знание уравнения механизма. [9]
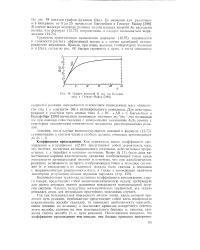 |
График функций и ( и ( по Бигелей-зеиу и Гепперт-Майер. [10] |
Количественная трактовка величины коэффициента прохождения, строго говоря, представляет собой квантовомеханическую задачу, требующую для своего решения знания уравнения поверхности потенциальной энергии системы. [11]
Из уравнений (2.83) следует, что для вычисления разности теплоем-костей Ср - Cv достаточно располагать лишь уравнением состояния; знание калорического уравнения не обязательно. [12]
Обсуждавшиеся в предыдущих разделах методы определения многоступенчатости реакций основаны на знании зависимости скорости реакции от концентрации каждого из реакционных компонентов; короче говоря, на знании уравнения скорости. [13]
При конструировании систем с заданными параметрами [152], выполнении расчетов тепловых и материальных балансов технологических процессов, а также в прогнозировании качества и свойств готового продукта необходимо знание уравнений суммарных реакций химического взаимодействия, протекающих в сложных системах. [14]
Основная задача изотермической динамики адсорбции в неподвижном слое адсорбента была сформулирована академиком М. М. Дубининым [6] и заключается в предвычислении основных функций процесса динамики адсорбции c ( L, t) и a ( L, t) на основе знания уравнения изотермы адсорбции и основных коэффициентов уравнения кинетики. Задача определения параметров изотермы ТОЗМ и эффективных коэффициентов внутренней диффузии на основе минимального экспериментального материала решена нами в предыдущих разделах. Здесь рассмотрим математическую модель однокомпонентной изотермической динамики адсорбции в неподвижном слое зерен адсорбента для реальных сорбционных процессов. Вообще, как и при моделировании любых физических процессов, в динамике адсорбции принято использовать модели различной сложности в зависимости от поставленной цели. [15]
Страницы: 1 2