Знание - уравнение
Cтраница 2
В большинстве задач по расчету реактора достаточно уравнений для стационарных состояний. Для расчета переходных режимов необходимо знание уравнений, описывающих динамику процесса. Для процессов с быстро изменяющейся активностью катализатора необходимо знать, кроме зависимости скорости реакции от температуры и концентрации реагирующих веществ, зависимость ее изменения от времени и условий проведения процесса. [16]
Если внешние условия, например статистические характеристики входных сигналов, как полезных, так и возмущений, и параметры объекта управления практически не изменяются в процессе работы или их изменения заранее известны, то для управления могут быть применены САУ с неизменяемыми характеристиками и алгоритмом управления. В этом случае априорной информации ( знание уравнений объекта и пределов возможного изменения его параметров, а также их зависимости от внешних условий), закладываемой при проектировании системы, достаточно для обеспечения требуемых показателей процесса управления. Вместе с тем в последнее время возникает необходимость обеспечения управления объектами при существенном и непредвиденном изменении их характеристики и характеристик входных воздействий, а также невозможности ( или большой сложности) их априорного определения. Например, при управлении летательными аппаратами приходится считаться с тем, что их характеристики не остаются неизменными вследствие изменения плотности атмосферы на разных высотах, скорости полета, веса и моментов инерции. [17]
Ибо дифференциальные уравнения прямейшего пути ( 158с) могут быть записаны явно, когда наряду с р заданы ав как функции рв. Для того чтобы прямейший путь материальной системы, положение которой определяется с помощью ре, выразить через уравнения для этих ре, достаточно, наряду со знанием уравнений условий для ре, знания любого бесконечно малого возможного перемещения как функции этих координат рв и их изменений. [18]
Наличие конфликтных ЧЕСТНЫХ критериев неизбежно приводит к гребневому характеру целевых функций, а наличие гребней существенно затрудняет поиск экстремума, делает его неэффективным и малонадежным при применении большинства известных методов поиска, в том числе при применении метода оврагов. С помощью максиминного критерия проблема решается потому, что здесь удается сформулировать уравнения гребней. В этом ключ к повышению эффективности поиска, так как знание уравнений гребней позволяет организовать движение по гребню в наилучшем направлении. В результате общее количество шагов снижается до уровня, приемлемого в условиях сложных математических моделей оптимизируемого объекта. [19]
 |
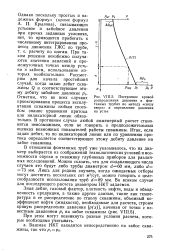
Построение кривой распределения давления в фонтанных трубах по методу снизу вверх и определение давления на устье. [20] |
При таком решении неизбежно получаются значения давлений в промежуточных точках между устьем и забоем, использование которых необязательно. Рассмотрим для начала простейший случай, когда задан дебит скважины Q и соответствующее этому дебиту забойное давление рс. Отметим, что во всех случаях проектирования процесса эксплуатации скважины любым способом знание уравнения притока или индикаторной линии обязательно. В противном случае любой инженерный расчет становится невозможным, если не говорить о предположительных оценках возможных показателей работы скважины. Итак, если задан дебит, то по индикаторной линии или по уравнению притока определяется соответствующее этому дебиту давление на забое скважины. [21]
 |
Построение кривой распределения давления в фонтанных трубах по методу снизу вверх и определение давления на устье. [22] |
При таком решении неизбежно получаются значения давлений в промежуточных точках между устьем и забоем, использование которых необязательно. Рассмотрим для начала простейший случай, когда задан дебит скважины Q и соответствующее этому дебиту забойное давление рс. Отметим, что во всех случаях проектирования процесса эксплуатации скважины любым способом знание уравнения притока или индикаторной линии обязательно. В противном случае любой инженерный расчет становится невозможным, если не говорить о предположительных оценках возможных показателей работы скважины. Итак, если задан дебит, то по индикаторной линии или по уравнению притока определяется соответствующее этому дебиту давление на забое скважины. [23]
Предполагая, что энтальпия пара постоянна, из уравнения ( 26) получаем соотношение между двумя переменными - it и Гй. Одна переменная может быть определена из этого уравнения, если известна другая. При существующем уровне знаний уравнения испарения этот метод оценки предпочтительнее, чем более строгий метод, изложенный в предыдущем разделе, так как он требует использования только одного предположения. Кроме того, как будет показано ниже, справедливость такого предположения, как аксиальное распределение температуры, может быть проверена экспериментально. [24]
Напорный ящик играет значительную роль в процессе производства бумаги. Он во многом влияет на формирование бумажного листа и веса 1 ма бумаги. Эти два фактора вместе со свойствами волокнистой массы определяют качество производимой бумаги. Поэтому системы регулирования для напорного ящика вызывают большой интерес среди специалистов, работающих в области бумажной промышленности. По этому вопросу уже опубликовано много исследований. Цель данного доклада заключается в предложении передаточных функций для напорного ящика с учетом гидравлических характеристик. Наиболее важным вопро-соы является математическое описание потока волокнистой массы. Поток ее зависит от потока жидкости, и поэтому знание уравнений гидравлики в напорном ящике - главное в математической модели входной части бумагоделательной машины, находящейся в воде. Требования к устройствам регулирования напорного ящика очень высоки. Регулируемая величина, суммарное давление напора должно поддерживаться в пределах 0 5 % от заданного значения. В системе отклонения различных переменных невелики относительно результатов установившегося состояния. Это означает, что процесс можно описать с помощью линейных передаточных функций. Постоянные этих функций зависят от значений величин в стационарном состоянии. Следовательно, нужно решить две задачи: определить виды передаточных функций и метод вычисления постоянных на основе известных параметров самой машины. Ниже рассматриваются передаточные функции процесса, происходящего в напорном ящике. Система управления испытана на специальном напорном ящике. Вся система смоделирована на аналоговой ВМ, вычислены кривые переходных характеристик. [25]
В предыдущих разделах было показано, что может быть вычислен теплообмен лобовой части цилиндра, у поверхности которой имеется пограничный слой. Кормовая часть поверхности находится в области разделенного потока, которая заполнена беспорядочными вихрями. В настоящий момент представляется невозможным произвести для этой части какие-либо расчеты конвективного переноса тепла. Остается только одна возможность: положиться на эксперимент и обобщать результаты путем анализа размерностей. Этот метод предполагает, что все физические процессы могут быть выражены в виде зависимости между безразмерными параметрами, и дает возможность найти эти параметры. В настоящее время есть несколько методов, при помощи которых могут быть определены безразмерные параметры, которые определяют какой-либо физический процесс. Наиболее важной и трудной частью анализа является нахождение не формы параметров, а их числа, которые полностью описывают рассматриваемый процесс. По своему опыту автор считает, что наиболее эффективным и верным путем получения ответа на этот вопрос является метод, который основывается и а дифференциальных уравнениях, описывающих процесс и преобразование их в безразмерные дифференциальные уравнения. Этот метод будет здесь применен. Может быть выдвинуто возражение, что в некоторых случаях могут быть неизвестны уравнения, описывающие процесс. Однако позже будет показано, что требуется только приблизительное знание уравнений, так как в противном случае нельзя произвести удовлетворительный анализ также и каким-нибудь другим методом. [26]
Страницы: 1 2