Ограниченная взаимная растворимость - компонент
Cтраница 2
В системе ZrB2 - СгВ2 можно было предположить ограниченную взаимную растворимость компонентов, так как Zr и Сг не образуют непрерывных рядов твердых растворов. Результаты, полученные при исследовании этих систем ( см. стр. В системе TiB2 - CrB2 был обнаружен непрерывный ряд твердых растворов, а в системе ZrB2 - СгВ2 установлена ограниченная взаимная растворимость компонентов. [16]
Более сложен расчет процесса, в системах с ограниченной взаимной растворимостью компонентов. [17]
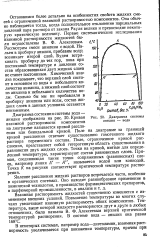 |
Диаграмма системы анилин - вода. [18] |
Остановимся более детально на особенностях свойств жидких смесей с ограниченной взаимной растворимостью компонентов. Она обычно наблюдается тогда, когда положительное отклонение парциальных давлений пара раствора от закона Рауля велико и превосходит некоторую критическую величину. [19]
 |
Равновесие жидкость - твердая фаза в бинарной системе с ограниченной взаимной растворимостью компонентов в жидком со-стоянии. [20] |
Существует и другой тип диаграмм плавкости систем, обладающих ограниченной взаимной растворимостью компонентов в твердом состоянии ( рис. V. В точке О жидкость находится в равновесии с двумя твердыми растворами, составы которых изображены точками XM и XN. Здесь система трехфазна и число степеней свободы системы при р const равно нулю. Следовательно, пока не исчезает одна из фаз, температура затвердевания То остается неизменной. [21]
 |
Равновесие жидкость - твердая фаза в бинарной системе с ограниченной взаимной растворимостью компонентов в твердом состоянии. [22] |
Теперь рассмотрим, как изображается графически состояние систем, обладающих ограниченной взаимной растворимостью компонентов в твердом состоянии ( рис. V. [23]
На рис. 46 приведены те же зависимости для системы с ограниченной взаимной растворимостью компонентов. В двухфазной области между равновесными концентрациями х и xz парциальные давления и активности каждого компонента одинаковы в обеих фазах. Когда общее давление достигает максимума, кривая общего давления имеет плоский участок. Этот случай соответствует образованию гетероазеотропной смеси. [24]
Для систем, образующих положительные азеотропы, наиболее объективные прогнозы возможны при ограниченной взаимной растворимости компонентов. Определение свойств бинарного гетсроазеотропа по данным о растворимости было рассмотрено вьдае. Для систем, образованных полностью смешивающимися веществами, имеющиеся в литературе указания, к сожалению, весьма неконкретны. Общей закономерностью является то, что чем больше различаются компоненты по химической природе и чем ближе их температуры кипения, тем более вероятно образование азеотроппой смеси. [25]
Из их диаграммы ( рис. 3) следует, что система характеризуется ограниченной взаимной растворимостью компонентов в твердом состоянии. [26]
На рис. XV-10, в приведена диаграмма равновесия бинарного расплава эвтектического типа при ограниченной взаимной растворимости компонентов в твердом состоянии. [27]
Представляется перспективным применение сочетания процессов кристаллизации и ректификации при разделении смесей, обладающих ограниченной взаимной растворимостью компонентов в твердом состоянии. Здесь ректификацию используют лишь для перехода через эвтектическую точку; выделение же целевых продуктов осуществляется кристаллизацией. [28]
Если кривая AGCM ( x2) имеет вид, изображенный на рис. 2 ( ограниченная взаимная растворимость компонентов), то смеси, мольные доли которых представлены точками на отрезках А Р и AZP, всегда стабильны. Фазы с составами между Р и Р, для которых кривая AGCM ( ж2) еще вогнута, как в точке с составом Р, стабильны по сравнению с разделением на фазы с близкими составами, но для разделения на составы, при котором соединяющая их линия пересекает PQ ниже точки Q, свободная энергия двухфазной системы меньше, чем гомогенной фазы. [29]
Если кривая AGCH ( x2) имеет вид, изображенный на рис. 2 ( ограниченная взаимная растворимость компонентов), то смеси, мольные доли которых представлены точками на отрезках А Р и А2Р, всегда стабильны. Фазы с составами между Р и Р, для которых кривая AGCM ( x2) еще вогнута, как в точке с составом Р, стабильны по сравнению с разделением на фазы с близкими составами, но для разделения на составы, при котором соединяющая их линия пересекает PQ ниже точки Q, свободная энергия двухфазной системы меньше, чем гомогенной фазы. [30]
Страницы: 1 2 3 4