Идеальный растворитель

Cтраница 3

Мы видим, что простая теория предсказывает для полимера в идеальном растворителе закон пропорциональности характеристической вязкости М1 / г. Это предсказание превосходно оправдывается на опыте. [31]

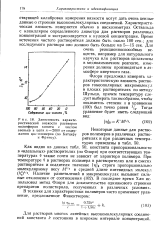Зависимость характеристической вязкости растворов полиэфиров хинита с числом звеньев в цепи я 2000 от содержания ч с-изомеров ( по Батцеру и Фритцу. [32]

Как видно из данных табл. 50, константа пропорциональности в идеальных растворителях ( по Флори) при соответствующих температурах б также почти не зависит от характера полимера. [33]

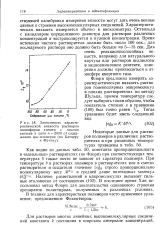Зависимость характеристической вязкости растворов полиэфиров хинита с числом звеньев в цепи 2000 от содержания ( uc - изомеров ( по Батцеру и Фритцу. [34]

Как видно из данных табл. 50, константа пропорциональности в идеальных растворителях ( по Флори) при соответствующих температурах 9 также почти не зависит от характера полимера. [35]

Для извлечения органических веществ из водных растворов эфир далеко не является идеальным растворителем, так как эфир и вода заметно растворимы друг в друге, кроме того, при подкис-лении водных растворов растворимость эфира в них резко повышается. Необходимо также избегать сильного встряхивания водных растворов с эфиром во избежание образования очень стойких, долго нерасслаивающихся эмульсий. [36]

Для извлечения органических веществ из водных растворов эфир далеко не является идеальным растворителем, так как эфир и вода заметно растворимы друг в друге, кроме того, при подкис-лении водных растворов растворимость эфира в них резко повы - ищется. Необходимо также избегать сильного встряхивания водных растворов с эфиром во избежание образования очень стойких, долго не расслаивающихся эмульсий. [37]

В этих в - условиях или, как говорят, в идеальном растворителе кон-формационные свойства цепи и ее средние квадратичные размеры ( h2) e контролируются только взаимодействиями ближнего порядка, и длинная цепочка имеет конформацию гауссового клубка. При этом эффективный исключенный объем обращается в нуль. [38]

Из опыта применения неводных растворителей в электрохимии следует, что не существует идеального растворителя. Однако имеются определенные физические и химические свойства, которые должны учитываться при выборе растворителя. Эти свойства могут широко изменяться при переходе от одного соединения к другому; соответственно для какого-то частного случая определенный растворитель может оказаться намного более подходящим, чем другие. [39]

N - число Авогадро; г - средний квадрат длины цепи в идеальном растворителе. [40]

Линденмейер [139], совпадение экспериментальных значений среднеквадратичного расстояния между концами цепи в идеальном растворителе, в котором объемные эффекты обращаются в нуль, с результатами расчета этой величины для бестелесных гауссовых цепей, допускающего самопересечение последних, не означает фактической реализации этой, физически не имеющей смысла, ситуации. Эти соображения, очевидно, полностью сохраняют силу и для разбавленных растворов дейтерированных цепочек в исходном ( протонированном) полимере, исследованных методом нейтронографии [84-92], несмотря на то. [41]

Для целей, преследуемых в данной главе, большую пользу может принести тот воображаемый идеальный растворитель, к представлению, о котором мы принуждены были обратиться, желая как-либо конкретизировать нулевое состояние газа. Вспомним, что главное свойство упомянутого воображаемого растворителя заключается в том, что раствор любой концентрации в нем подобен идеальному газу. Сверх того, ради удобства можно наделить наш идеальный растворитель свойствами абсолютной несжимаемости, нетеплоемкости, невесомости и еще тем свойством, что молекулы растворенного вещества движутся в нем, не испытывая сопротивления со стороны среды растворителя, как в вакууме. В таком виде назовем этот идеальный растворитель а-фазой, а растворенное в нем вещество ( л-паром. [42]

Как уже указывалось, мерой гибкости макромолекул являются их размеры в 6-точке ( идеальном растворителе), в которой влияние взаимодействий дальнего порядка отсутствует. Для определения этих размеров нужно либо проводить измерения непосредственно в в-точке, либо исключать влияние взаимодействий дальнего порядка с помощью существующих теорий. [43]

Такая ситуация, соответствующая исчезновению эффекта исключенного объема, реализуется в так называемых идеальных растворителях только при определенной температуре, которая по физическому смыслу полностью аналогична точке Бойля для реальных газов. Эта температура носит название в-точки, или температуры Флори, а конформационное состояние макромолекулы в этих условиях называется невозмущенным. [44]

Поэтому полученные в указанных работах значения Ф относятся, строго говоря, только к идеальному растворителю, в котором объемные эффекты отсутствуют. [45]

Страницы: 1 2 3 4