Значение - дисперсия
Cтраница 3
Приводя столь резкое различие значений дисперсии, автор подчеркивает влияние гидродинамики и прежде всего входных условий на процесс перемешивания, а следовательно, и на процесс горения газовых смесей. Сразу же заметим, что если В. А. Баум указывает на независимость процессов смешения от критерия Рейнольдса, то А. Г. Прудников все построение своей теории перемешивания и горения гомогенных смесей базирует на зависимости эффективности смешения и горения от критерия Рейнольдса. Таким образом, существуют определенные расхождения в вопросе о влиянии на протяженность зоны смесеобразования гидродинамических параметров и прежде всего критерия Рейнольдса. [31]
Особо следует сказать о вычислении значения дисперсии при статистических расчетах. Поскольку для вычисления стандартной погрешности s или доверительных границ необходимо извлекать квадратный корень из величины s2, последняя должна быть определена с максимальным числом правильных значащих цифр. [32]
Сравнивая это значение дисперсии со значением дисперсии для статического режима, которое равно 0 16 В2, видно, что дисперсия для динамического режима меньше, чем для статического. Причина этого заключается в том, что инерция СИ, представленная параметром Т, уменьшает разброс возможных значений результата измерения. [33]
Таким образом, можно предварительно найти значение дисперсии у во всем диапазоне ее измерения при будущих совместных измерениях. Если она окажется постоянной, то измерения будут равноточными, если переменной - то нерав-ноточными, но вес каждого из них, определяемый отношением 1 I с2 будет известен. [34]
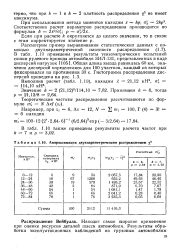 |
Аппроксимация двухпараметрическим распределением х2. [35] |
Общая длина заезда равнялась 60 км, значения дисперсий определялись для 100 участков, каждый из которых фиксировался на протяжении 30 с. [36]
Для вычисления по этой формуле предварительно находят значения дисперсий s2 в каждой из i точек. [37]
Параметр о характеризует предельное ( максимальное) значение дисперсии. Вероятность взятия пробы с концентрацией с 1 равняется доле анализируемого компонента в смеси или концентрации сср. Вероятность взятия пробы с концентрацией с / 0 равняется 1 - сср. [38]
Часто экспериментатор перед началом измерений не знает значения дисперсии результатов наблюдений. В этом случае параметры распределения в виде их оценок определяют непосредственно из опытных данных. [39]
И наоборот, когда точность измерения невелика, значения дисперсий 3qq a получаются большими, а веса маленькими. Ясно, что чем больше вес, тем сильнее влияние на величину критерия F2 различных по величине значений т)) и у 9, и, следовательно, тем меньше будут отклонения найденных констант от их вероятных значений. Поэтому непременным условием испол-ьзования критерия F2 является высокая точность измерения наблюдаемых величин в опытах. [40]
Каково увеличение ожидаемых средних затрат, обусловленное недооценкой значения дисперсии на интервале упреждения. [41]
Аналогичным образом обстоит дело с проверкой гипотезы о значении дисперсии нормальной выборки. [42]
Рассмотрим интервальную оценку функции отклика для случая, когда значение дисперсии Df известно. [43]
Заметим, что если число N возрастает, то значение дисперсии портфеля почти приближается к среднему значению ковариации. [44]
Заметим, что если число W возрастает, то значение дисперсии портфеля почти приближается к среднему значению ковариации. [45]
Страницы: 1 2 3 4