Значение - долговечность
Cтраница 2
Проведенные исследования свидетельствуют о высоком рассеивании значений долговечности для титановых сплавов. Большое рассеивание наблюдается не только при действии переменных напряжений, близких по уровню к пределу выносливости, но и на уровнях, значительно его превышающих. [16]
У этих сталей наблюдается значительное рассеяние значений долговечности: отдельные образцы не разрушились после 720 ч испытаний даже на уровне арн 2 ГПа. [17]
Опыты показали, что разница в значениях долговечности невелика, если за критерий принять наибольшие растягивающие напряжения. Поверхность разрушения во всех случаях совпадает с плоскостью их действия. Поэтому можно полагать, что независимо от характера разрушения ( хрупкое или пластичное) за него ответственна шаровая часть тензора напряжений, и только положительная. В первом приближении за критерий долговечности можно принять наибольшее растягивающее напряжение ах. [18]
Расчет по линейной гипотезе суммирования повреждений дает значения долговечности, на порядок и более превышающие экспериментальные. Наибольшая корреляционная связь наблюдается между долговечностью и суммарными растягивающими деформациями с учетом перераспределения деформаций вследствие процессов пластичности и ползучести. [19]
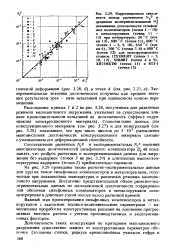
Сопоставление расчетных NfP и экспериментальных N 3 значений мало цикловых долговечностей сильфонного компенсатора Д 40 показывает, что разброс расчетных и экспериментальных данных для нагружения без выдержек ( точки 3 на рис. 3.29) и длительных высокотемпературных выдержек ( точки 2) приблизительно одинаков. [21]
Таким образом, можно считать, что приведенные ниже значения долговечностей соответствуют зарождению трещин размером 1 - 1 5 мм. [22]
В силу случайности параметров бис уравнения ( 20) значения долговечности целесообразно рассчитывать методом Монте-Карло, процедура которого в данном случае предусматривает следующее. [23]
Сопоставление экспериментальных и расчетных ( по уравнению 4.18) значений долговечности для стали 37Х12Н8Г8МФБ приведено в табл. 4.5. Как видно, расчет в основном дает несколько меньшие значения долговечности. [24]
Правильность гипотезы накопления повреждения оценивается в конечном итоге по совпадению значений долговечности, полученных при программных испытаниях и предсказанных данной гипотезой. Предполагается, что гипотезой, а по существу - способом вычисления повреждения, можно пользоваться при других режимах нагружения, в том числе эксплуатационных, так как она дает расчетную оценку усталостного повреждения на всех стадиях его роста. Установление границ применимости и численная оценка погрешностей, связанных с выходом за пределы этих границ, имеют практическое значение. [25]
Индексирование ступеней нагрузки GJ, соответствующих циклов нагружения щ а также значений долговечности NJJ принято таким, что первый индекс j 1 обозначает ступень напряжения в предусмотренной последовательности, а второй i 0 - соответствующую кривую а - N. Начиная с исходной кривой усталости ( г 0) затраченное при Oj 04 число циклов нагружения щ rai. Такое направление поворота означает разупрочнение материала вследствие предшествующей усталостной нагрузки. [26]
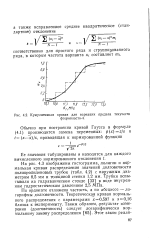 |
Кумулятивная кривая для вариации предела текучести. [27] |
На рис. 4.3 изображены гистограмма, полигон я нормальная кривая распределения значений долговечности полипропиленовых трубок ( табл. 4.2) с наружным диаметром 8 5 мм и толщиной стенки 1 2 мм. [28]
По данным ряда исследователей [131, 132, 135], для алюминиевых сплавов характерен значительный разброс значений долговечности, определяемых при усталостных испытаниях. С увеличением уровня напряжения это отношение уменьшается. В связи с этим исследование усталости алюминиевых сплавов необходимо проводить в статистическом аспекте: на каждом уровне напряжений испытывать большое число образцов и результаты испытаний обрабатывать существующими методами математической статистики, а характеристики выносливости оценивать по условию вероятности. [29]
Страницы: 1 2 3 4 5