Значение - интеграл
Cтраница 1
Значение интеграла с переменным верхним пределом раскрывает следующая теорема. [1]
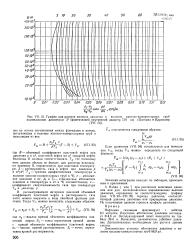 |
График для расчета. падения давления в колонне насосно-компрессорных труб номинальным диаметром 3 ( фактический внутренний диаметр 7 81 см ( Пигпмен и Карпентер. [2] |
Значения интегралов находят по таблицам, приведенным в приложении. [3]
Значение интеграла, входящего в выражение надежности, можно рассчитать лишь численными методами с помощью ЭВМ, пользоваться этим выражением для нахождения искомого К крайне неудобно. [4]
Значение интеграла в формуле (11.20) находят методом численного или графического интегрирования. [5]
Значение интеграла может быть определено графически. [6]
Значение интеграла в уравнении (XI.7) определяется графическим способом. [7]
Значение интеграла в пределах от хг 0 6 до х2 0 05 изображается заштрихованной площадью. Эта площадь равна 403 мма. [8]
Значение интеграла в формуле (2.84) находят методом численного или графического интегрирования. [9]
Значения интеграла ( 5) приводятся в таблицах. Расчет гранулометрического состава по этому уравнению еще не получил широкого распространения применительно к измельчению угля. [10]
Значение интеграла рассчитывается графически. [11]
Значение интеграла в уравнении (2.25) для сложных зависимостей р ( у) может быть найдено приближенными методами в качестве функции нижнего предела. [12]
Значение интеграла в (1.39) рассчитывается или аналитически, если экспериментальные данные описаны уравнением состояния, или при помощи графоаналитических методов. [13]
Значение интеграла находится многократным интегрированием по частям. [14]
Значения интегралов в правых частях уравнений (11.49) обычно определяются графически, ибо равновесная зависимость у ty ( x) редко имеет настолько простой вид, чтобы можно было непосредственно интегрировать эти выражения. Каждое из них представляет собой проинтегрированное отношение изменения концентрации к движущей силе, вызывающей это изменение. [15]
Страницы: 1 2 3 4