Значение - интеграл
Cтраница 2
Значения интегралов в выражениях (8.3) и (8.4) можно легко найти, используя простейшие графо-аналитические методы. [16]
Значение интеграла не зависит от выбора контура Г, обладающего описанными свойствами, и представляет собой линейный ограниченный оператор, зависящий от выбора оператора А. [17]
Значение интеграла / is не может быть отрицательным, поскольку подынтегральная функция х18ех - 1 на всем отрезке интегрирования [0,1] неотрицательна. Это и приводит к результату, не имеющему смысла. [18]
Значение интеграла не зависит от пути интегрирования, целиком принадлежащего верхней полуплоскости и соединяющего точки 0 и оо, в чем убеждаемся путем предельного перехода, исходя из интегральной теоремы Коши. Отсюда и вытекает непрерывность рассматриваемой функции w ( z) в точке z оо. [19]
Значение интеграла представляет площадь, ограниченная кривой, осью абсцисс и пограничными ординатами. [20]
Значения интеграла рассчитаны из величин a ( fe), измеренных вблизи точки плавления. [21]
Значение интегралов ( 163) и ( 164) не зависит от употребляемой системы координат и импульсов, так же как и значение тех же интегралов без множителя е следовательно, значение i p также не должно зависеть от системы координат и импульсов. [22]
Значение интегралов в уравнении (III.45) было вычислено в разделе 1 настоящей главы для двух эмпирических зависимостей между коэффициентом сжимаемости пор и эффективным давлением. [23]
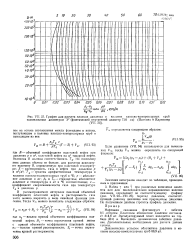 |
График для расчета падения давления в колонне насосно-компрессорных труб номинальным диаметром 3 ( фактический внутренний диаметр 7 81 см ( Питтмен и Кярпентер. [24] |
Значения интегралов находят по таблицам, приведенным в приложении. [25]
Значения интегралов находятся путем численного интегрирования. [26]
Значение интеграла, находящегося в правой части последнего равенства, может быть найдено различными способами. [27]
Значение интеграла в (8.11) определяется зависимостью длины свободного пробега / от энергии. [28]
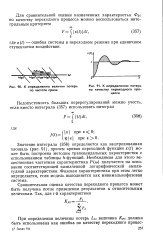 |
К определению величин потерь по частоте среза.| К определению потерь по качеству переходного процесса. [29] |
Значение интеграла ( 358) определяется как заштрихованная площадь ( рис. 91), причем кривая переходной функции x ( t) может быть построена методом трапецеидальных характеристик с использованием таблицы / i-функций. Необходимая для этого вещественная частотная характеристика Р ( ш) получается на основании соответствующей назначенной логарифмической амплитудной характеристики. Фазовая характеристика при этом легко определяется, если модель выполняется как минимальнофазовая система. [30]
Страницы: 1 2 3 4