Расходы - фаза
Cтраница 1
Расходы фаз постоянны по высоте аппарата, например в процессах ректификации, когда числа молей компонентов, которыми обмениваются фазы, равны. [1]
Чаще мольные расходы фаз в исчерпывающей части определяют, исходя из теплового баланса для тарелки питания. [2]
Влияние расходов фаз и соотношения нагрузок на Е % не обнаружено. Это подтверждает высказанную ранее мысль, что снижение коэффициента продольного перемешивания Ея с увеличением частоты и амплитуды пульсации вызвано изменением структуры потока, а именно, изменением размера капель и их однородности, а также их поведением в потоке. [3]
При равенстве расходов фаз ( G L) полюс, соответствующий выражениям ( с) и ( у), лежит на бесконечном удалении от треугольника, а лучи параллельны друг другу. При уменьшении отношения L / G полюс смещается влево. Проанализируем, как смещение полюса отражается на движущей силе процесса массопередачи. [4]
 |
Обозначения для составов и расходов фаз. [5] |
В этих уравнениях расходы фаз должны быть массовыми, если концентрации выражены в масс, долях; при выражении составов в мол. [6]
 |
Построение прямых VHQ ( I - - Ф - PCOV при значениях vn0 и vc0, выходящих за пределы значений, отложенных на осях графика Щ. [7] |
Сравнение экспериментальных значений расходов фаз при захлебывании для стеклянных шариков диаметров 0 465 мм и 0 82 мм, осаждающихся в воде [147], с кривыми, рассчитанными по предлагаемой методике, приведено на рис. 2.7. Как следует из рисунка, совпадение результатов вполне удовлетворительное. [8]
При применении этого метода мольные расходы фаз в каждой из частей колонны принимают постоянными. [9]
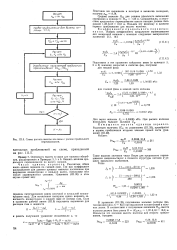 |
Схема расчета высоты колонны с учетом продольного перемешивания. [10] |
В уравнение (III.39) подставлены мольные расходы фаз, так как величина от 82 5 при выражении концентраций в мольных долях. [11]
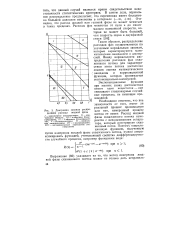 |
Диаграмма законов распределения расхода жидкой фазы. [12] |
Таким образом, распределение расходов фаз осуществляется по усеченным нормальным законам, которые характеризуются математическим ожиданием и дисперсией. Ввиду нормальности распределения расходов фаз скважинного потока для характеристики этого потока достаточно знания оценки математического ожидания и корреляционной функции, которая принимается экспоненциально-косинусной. [13]
В тех случаях, когда расходы фаз постоянны во времени, удельные объемы каждой фазы и скорости фаз также постоянны. [14]
Таким образом, если при противотоке расходы фаз равны, то при отсутствии теплообмена со внешней средой конноды параллельны. [15]
Страницы: 1 2 3 4