Еще большее расхождение

Cтраница 2

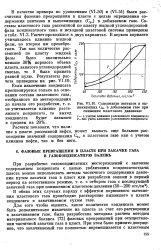Содержание пентанов и вышекипящих СБ в добываемом газе при снижении пластового давления. [16]

Расчеты показали, что наличие в пласте рассеянной нефти, может вызвать еще большее расхождение значений содержания С5 в пластовом газе как с учетом влияния нефти, так и без него. [17]

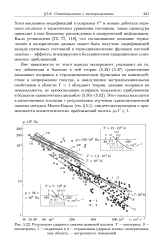Результаты ударного сжатия цезиевой плазмы. Т - изотермы. S - изоэнтропы. 1 - падающая и 2 - отраженная ударные волны. заштрихованная область - погрешность измерений. [18]

Хотя введением модификаций в поправки Fc и можно добиться хорошего согласия в термическом уравнении состояния, такая процедура приводит к еще большему расхождению в калорической информации. Было установлено [73, 77, 118], что согласованное описание термических и калорических данных может быть получено модификацией вклада связанных состояний в термодинамические функции плотной плазмы - эффекта, игнорируемого большинством традиционных плазменных приближений. [19]

Цены на угли одной и той же марки и качества в пределах угольного бассейна существенно различаются, причем эти различия порой достигают 40 - 80 %, еще большие расхождения отмечаются в оценке стоимости 1 ккал / кг - почти в 2 раза. Цены на угли менее ценных ( так называемых мелких классов) растут быстрее, чем на угли крупно-средних классов, достигая уровня последних. Аналогичное положение складывается и с оценкой потребительских свойств коксующихся углей. Так, в Кузнецком бассейне на марки коксующегося угля, имеющие разные коэффициенты технологической ценности, устанавливаются одинаковые цены, а у отдельных производителей цены на менее качественные угли могут быть даже выше, чем на более качественные коксующиеся угли у других производителей. [20]

Уравнение Борна, выведенное и примененное вначале к расчетам энергетики процессов растворения электролитов в воде, пытались также использовать для неводных растворов, однако в этом случае наблюдались еще большие расхождения теории с экспериментом. [21]

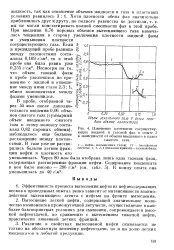Изменение плотности сосуществующих жидкой и газовой фаз в опыте 3 в зависимости от объема введенного в пласт сжатого газа. [22]

В пробе, отобранной через 55 мин после дополни - § тельного введения 0 06 объемов сжатого газа ( суммарный объем введенного сжатого газа к этому моменту составлял 0 82 поровых объема), наблюдалось еще большее расхождение между плотностями. [23]

Однако для сравнительно высоких температур получается значительное несоответствие приведенных значений темплоемкостей двухатомных газов с экспериментальными данными. Еще большее расхождение получается для трех - и многоатомных газов. [24]

В этом случае наблюдается еще большее расхождение оценок в зависимости от принятого способа определения. Например, машина МИР может считать с точностью до 6 десятичных знаков и с точностью до 100 десятичных знаков. Соответственно, разброс по времени выполнения операции сложения может достигать нескольких порядков. В этом случае вообще трудно говорить о среднем времени выполнения операций или о среднем быстродействии. [25]

Сплошная линия изображает те же величины, полученные по методу конечных элементов. Как видим, расхождения в перемещениях довольно значительны, особенно вблизи точек приложения сосредоточенных сил. В других точках наблюдаются еще большие расхождения. [26]

Авторы этого исследования отметили ненадежность уравнения Кельвина для вычисления радиуса капилляров по изотермам адсорбции воды из-за допущений относительно величины угла смачивания стенок капилляров водой. Так, например, если принять, как обычно, что угол смачивания водой и метиловым спиртом равен нулю, то расчет по изотермам сорбции паров этих жидкостей дает весьма различные распределения пор по размерам их радиусов. Применение более вероятных величин для этого угла приводит к еще большему расхождению результатов. [27]

Величина рА этого буфера изменяется мало и не уменьшается, как в в случае растворов НС1, а несколько возрастает. Из рис. 106 следует также, что ни Н0, ни Я () не передают действительного хода зависимости единой кислотности с изменением растворителя. Более того, Н ( -) одного и того же раствора, измеренная с помощью различных индикаторов [ 2 4-динитрофенол ( Я ()) и димедон ( Н ( -)), расходятся. Еще большее расхождение между рА, Н0 и ( для растворов сильных кислот, где они разнятся на 2 - 4 единицы. [28]

Из табл. 11 видно, что для воды коэффициент затухания, подсчитанный для линейного закона трения К, достаточно хорошо совпадает с коэффициентом затухания К, полученным экспериментально. Это совпадение не наблюдается для квадратичного закона трения. Кроме того, из табл. 11 видно, что с увеличением предельного напряжения сдвига и структурной вязкости глинистого раствора расхождение экспериментальных данных с теоретическими становятся значительными. При этом квадратичный закон трения дает еще большее расхождение. [29]

В отличие от этого рНр ацетатного буфера сильно возрастают в связи со значительным ослаблением силы кислоты. Величина рА этого буфера изменяется мало и не уменьшается, как в случае растворов НС1, а несколько возрастает. Из рис. 117 следует также, что ни Я, ни Я ( не передают действительного хода зависимости единой кислотности с изменением растворителя. Более того, Я ( одного и того же раствора, измеренная с помощью различных индикаторов [ 2 4-динит-рофенол ( Я ()) и димедон ( Я ()) 1, расходятся. Еще большее расхождение между рА, Я0 и Я () для растворов сильных кислот, где они разнятся на 2 - 4 единицы. [30]

Страницы: 1 2 3