Расчет - интеграл
Cтраница 3
По каждой переменной может быть выбран свой метод расчета одномерного интеграла. Точность расчета многократного интеграла будет зависеть от точности вычисления соответствующих однократных интегралов, поэтому необходимо выбрать наиболее точный метод расчета однократного интеграла. [31]
Преимущество этого способа решения линейной системы по сравнению с расчетом интеграла от матричной экспоненты с использованием рекурренты (5.46) состоит в выигрыше необходимого числа операций. Однако в вычислении по формуле (5.57), на наш взгляд, есть два суще-ственых недостатка. [32]
Если решение задачи на самосогласование не вызывает серьезных затруднений, так же как и расчет интегралов Spv и Ну. Хт) стоит в неэмпирических расчетах весьма остро. [33]
Совершенно ясно, что оценка / ( А) будет плохой, если проводить независимые расчеты интегралов. Поэтому целесообразно использовать одни и те же случайные числа для всех интересующих значений К. Такой способ расчета принято называть методом зависимых испытаний. [34]
Это предсказание не зависит от вида радиальных частей орбит, используемых при вычислении различных встречающихся в расчете интегралов. [35]
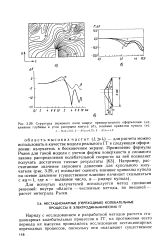 |
Структура звукового поля вокруг прямоугольного оформления ( а. влияние глубины и угла раскрыва конуса ( б, влияние кривизны купола ( в. [36] |
Для вогнутых излучателей используется метод сшивания решений: внутри области - численные методы, во внешней - расчет интеграла Рэлея. [37]
Ячеечно-групповая теория является лучшим приближением, чем теория свободного объема, но во всех вариантах ячеечного метода расчета интеграла по состояниям предполагается известной структура жидкости, по крайней мере известно строение ближней координационной сферы. Расположение центров ячеек может соответствовать различным типам решеток, но всегда предполагается, что эти ячейки жестко закреплены в пространстве. Хаотическое распределение молекул, изотропность жидкости обусловлены в этих теориях лишь нарушением дальнего порядка в решетке. Возможные попытки построить теорию функции распределения атомов на основании таких ячеечных представлений должны быть основаны на идее существования нерегулярной, но жесткой решетки, узлы которой являются центрами ячеек. [38]
Ячеечно-групповая теория является лучшим приближением, чем теория свободного объема, но во всех вариантах ячеечного метода расчета интеграла по состояниям предполагается известной структура жидкости, по крайней мере известно строение ближней координационной сферы. Расположение центров ячеек может соответствовать различным типам решеток, но всегда предполагается, что эти ячейки жестко закреплены в пространстве. Хаотическое распределение молекул, изотропность жидкости обусловлены в этих теориях лишь нарушением дальнего порядка в решетке. Возможные попытки построить теорию функции распределения атомов на основании таких ячеечных представлений должны быть основаны на идее существования нерегулярной, но жесткой решетки, узлы которой - являются центрами ячеек. [39]
Так же как и в теории чистых жидкостей, главная трудность в статистической теории растворов связана с расчетом интеграла состояний. Мы уже отмечали, что точное вычисление интеграла состояний в тех случаях, когда молекулы взаимодействуют друг с другом, сопряжено с математическими трудностями, до сих пор еще не преодоленными. Поэтому расчет интеграла состояний осуществляется при помощи различного рода приближенных методов. С целью облегчения расчета реальная модель раствора заменяется идеализированной, упрощенной моделью, причем в различных вариантах теории упрощения, как увидим, бывают разными. [40]
 |
Диаграмма уровней энергии для я-системы триметиленметана ( метод МОХ. [41] |
Высшая молекулярная орбиталь А2 ( 2), сильно разрыхляющая, по-видимому, существенно не используется, хотя расчетов интегралов, перекрывания не производилось. [42]
Таким образом, важнейшей задачей в расчетах по методу Рутаана является нахождение наиболее удачного компромисса между размером базиса и числом подлежащих расчету интегралов. [43]
Здесь и в таблице 4.3 Ткр, ркр, VKp - критическая температура, плотность и молярный объем; е - силовая постоянная для расчета интеграла столкновений Q; k - постоянная Больцмана. [44]
Предположим, что известно, как преобразуются порознь функции фт и фп теперь определим, как преобразуется их произведение фтфп. Расчет интегралов от произведения будет рассмотрен позднее. [45]
Страницы: 1 2 3 4