Расчет - дифракционная картина
Cтраница 2
Помимо своего теоретического значения, указанная теорема особенно важна с вычислительной точки зрения, поскольку, как правило, расчет когерентности оказывается более трудным, чем расчет соответствующей дифракционной картины. [16]
Существует ряд специальных методов, которые тем не менее позволяют преодолеть трудности, связанные с определением фаз. В случае простых молекул производят расчет дифракционной картины для предполагаемой модели исследуемой структуры и эту рассчитанную картину сравнивают с экспериментальной. [17]
Плоская волна проникает в профилированный штрих, причем отдельные его элементы создадут запаздывание по фазе, так как волновая поверхность достигнет разных участков штриха в различные моменты времени. Это запаздывание по фазе следует учитывать при расчете дифракционной картины. Оно приводит к тому, что функцию ( sinu / u) 2 в выражении (6.49) нужно заменить другой, более сложной функцией, зависящей от геометрии штриха. [18]
Изложенное в § 50 ( и, в частности, установленная Рэлеем особенность дифракции на синусоидальных решетках, дающих спектры только первого порядка) позволяет весьма общим и практически важным способом рассмотреть вопрос о дифракции на структурах любого вида. Какова бы ни была структура ( в частности, даже если она не периодична), явления дифракции имеют место. Расчет дифракционной картины в таком практически очень распространенном случае, однако, гораздо труднее. [19]
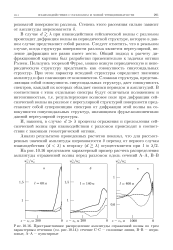 |
Пространственное распределение амплитуды отраженной волны по трем характерным сечениям (. сечение С-С - сплошные линии, В-В - штриховые, А-А - пунктирные. [20] |
В случае d А при взаимодействии сейсмической волны с разломом происходит дифракция волны на периодической структуре, которую в данном случае представляет собой разлом. Следует отметить, что в реальном случае, когда структура поверхности разлома является нерегулярной, явление дифракции все равно имеет место. Общий подход к расчету дифракционной картины был разработан применительно к задачам оптики Рэлеем. Пользуясь теоремой Фурье, можно всякую периодическую и непериодическую структуру представить как совокупность синусоидальных структур. При этом характер исходной структуры определяет значения амплитуд и фаз слагающих ее компонентов. Сложная структура, представляющая собой совокупность синусоидальных структур, дает совокупность спектров, каждый их которых обладает своими периодом и амплитудой. В соответствии с этим отдельные спектры будут отличаться положением и интенсивностью, т.е. результирующее волновое поле при дифракции сейсмической волны на разломе с нерегулярной структурой поверхности представляет собой суперпозицию спектров от дифракции этой волны на совокупности синусоидальных структур, являющихся фурье-компонентами данной нерегулярной структуры. [21]
Этот интеграл в общем случае не так-то просто взять. Задача, однако, упрощается при наличии какой-либо симметрии. Одним из простых примеров является расчет дифракционной картины от круглого отверстия. [22]
 |
Дифракционные явления.| Эффекты дифракции в области тени. Экспонирование позитивного фоторезиста ФП-383 с применением цветного фотошаблона. Время экспонирования. / - 4. 2 - 6. 3 - 8. 4 - 14. [23] |
В данном случае происходит интерференция двух лучей - прошедшего через окрашенный слой и дифрагировавшего на краю элемента, в связи с чем вдоль краев элементов в области тени располагаются чередующиеся светлые и темные полосы. Здесь же показано, что расстояние от края тени до первого максимума ( или минимума) интенсивности светового сигнала пропорционально Yh, что свидетельствует о дифракционной природе явления. Гюйгенса - Френеля был проведен расчет дифракционной картины распределения света для топологических элементов в виде квадратов и прямоугольников. [24]
Наличие любых искажений прежде всего уменьшает четкость дифракционной картины ( интенсивность и остроту рефлексов), а это быстро приводит к практическому исчезновению ряда рефлексов, слиянию близлежащих рефлексов, увеличению диффузного фона, что, в свою очередь, снижает эффективность прямого анализа, уменьшая точность и обедняя получаемую структурную картину. Поэтому, если для таких объектов, как низкомолекуляр-яые жидкости, сравнительно простая задача определения характеристик ближнего порядка еще могла решаться методом прямого анализа дифракции, то для. В этом методе задают те или иные модели искажений и производят расчеты дифракционных картин с варьируемыми параметрами структуры. Затем экспериментальные и рассчитанные дифракционные картины сравнивают и по результатам сравнения делают заключения о типе структуры и ее искажениях в исследованном полимерном объекте, а также определяют количественные значения параметров искаженной структуры. [25]
В задачах, связанных с дифракцией света, используется теория Френеля - Гюйгенса. Согласно этой теории, любая точка пространства, до которой дошел фронт волны, представляет собой вторичный ( виртуальный) источник; все виртуальные источники когерентны; наблюдаемое распределение интенсивности есть результат интерференции вторичных волн. Метод зон Френеля и векторное сложение колебаний, используемые при решении задач, естественно приводят к тому, что расчет дифракционной картины является приближенным. [26]
Страницы: 1 2