Расчет - критическая нагрузка
Cтраница 2
Однако, когда направление роста трещины заранее не очевидно, в энергетическом подходе возникают аналитические трудности. Поэтому расчет критических нагрузок проделан лишь для немногих задач о симметричных трещинах. Кроме того, подход Гриффита требует рассмотрения энергии всей системы в целом. [16]
 |
Двухслойная стенка. [17] |
Для расчета критической нагрузки необходимо знать жесткости стенок в продольном / и кольцевом 2 направлениях. [18]
Применяющиеся в трехслойных оболочках заполнители имеют различную структуру: сплошные из однородного материала, перфорированные, сотовые и ребристые. При расчете критической нагрузки необходимо знать жесткость заполнителя на сдвиг. [19]
Если конструкция содержит достаточно большое количество слоев, можно перейти от анализа устойчивости пакета как дискретной системы к уравнениям сплошной среды с приведенными упругими параметрами. Путем сопоставления результате расчета критических нагрузок многослойной колонны по дискретной и непрерывной моделям авторы пришли к выводу, что с приемлемой для технических приложений 6 % - ной точностью использование континуальной теории возможно при числе резиновых слоев больше десяти для колонн с защемленными концами и более пяти для колонн с шарнирно опертыми концами. [20]
Отметим, что метод Б.Я. Пинеса позволяет находить критические нагрузки с точностью до постоянного множителя. Последний используется при расчетах критических нагрузок, проводимых с помощью описанного выше приема. [21]
При выборе коэффициента безопасности сжатых элементов принимают во внимание ряд дополнительных факторов, влияющих на несущую способность. Как правило, подобные факторы учитываются при расчете критической нагрузки соответствующим выбором коэффициента устойчивости. [22]
 |
Исходные данные. [23] |
Следует отметить, что при осевом равномерном сжатии изотропных цилиндрических оболочек значение критической нагрузки, полученной по линейной теории, плохо согласуется с результатами экспериментов. Для слоистых оболочек соответствие данных экспериментов с результатами расчетов критической нагрузки по линейной теории более удовлетворительное, а разброс экспериментальных данных не столь велик, как в случае тонких изо-тройных оболочек. [24]
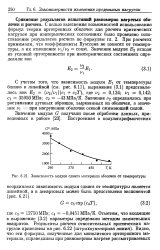 |
Зависимость модуля сдвига материала оболочек от температуры. [25] |
С целью выяснения возможностей использования формул теории ортотропных оболочек для расчета критических нагрузок при изотермических состояниях было проведено сопоставление результатов расчета по формулам гл. [26]
Исследованиям кризиса кипения жидкости, движущейся в трубах и каналах, посвящено большое число работ. Поэтому расчет критических нагрузок здесь следует проводить по непосредственным ( частным) данным, полученным из опытов с такими же жидкостями и в соответствующих условиях. [27]
Страницы: 1 2