Расчет - пластина
Cтраница 2
Для расчета пластин и других тонкостенных конструкций сложной конфигурации МКЭ является наиболее перспективным методом, позволяющим получить исчерпывающую информацию о деформированном и напряженном состоянии конструкции. [16]
Для расчета пластины воспользуемся теорией малых упруго-пластических деформаций, предполагая тем самым такое приложение внешней поперечной нагрузки q x, у), при котором во всех точках пластины осуществляется простое нагружение или близкое к нему. [17]
Для расчета пластин с криволинейным контуром целесообразно значени внутренних сил и моментов выразить через производные прогиба по нормали к контуру и вдоль него. [18]
Для расчета пластин и других тонкостенных конструкций сложной конфигурации МКЭ является наиболее перспективным методом, позволяющим получить исчерпывающую информацию о деформированном и напряженном состоянии конструкции. [19]
Для расчета пластин на изгиб метод Бубнова-Галеркина является менее эффективным, чем метод Ритца, так как обычно трудно подобрать координатные функции, удовлетворяющие веем граничным условиям, а в случае пластин переменной толщины сложный вид имеют дифференциальные уравнения изгиба. [20]
Для расчета пластин ступенчатого профиля и пластин со сложным нагружением целесообразно применение ЭВМ. [21]
При расчете пластин по методу ri конечных разностей плоскость пла - mj стины покрывают сеткой пересекающихся линий. Рассмотрим не - У которую точку / С, расположенную на пересечении линий, обозначенных буквами тип. [22]
При расчете пластин вводятся понятия о срединной плоскости и линейном элементе. Плоскость, которая делит пла: стину пополам по толщине, называется срединной плоскостью. [23]
При расчете пластин на прочность наибольшую опасность представляют нормальные напряжения ох и ау и касательное напряжение тху. Напряжения xzx, xzy и az, как правило, значительно меньше напряжений ох, ау и хху и мало влияют на оценку прочности пластины. [24]
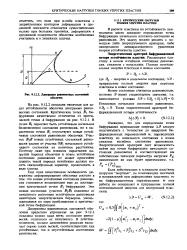 |
Диаграмма равномсных состояний оболочек. [25] |
В расчете пластины на устойчивость центральное место занимает определение точек бифуркации начального плоского состояния ее равновесия. [26]
При расчете пластин считается, что прогиб w существенно меньше толщины пластины / г. Именно в этом предположении можно изгиб пластины рассматривать независимо от растяжения. Пластины, удовлетворяющие этому условию, называют иногда тонкими плитами. [27]
 |
Приведение многослойной балки - полоски к однослойной ( пояснения в тексте. [28] |
При расчете пластин и оболочек из многослойного ортотропно-го композита метод приведенного сечения неудобен. [29]
При расчете пластин постоянной толщины, нагруженных произвольной осесимметричной нагрузкой, нагрузку обычно схематизируют. [30]
Страницы: 1 2 3 4