Расчет - пластина
Cтраница 3
При расчете пластин постоянной толщины, нагруженных произвольной осесимметричной нагрузкой, нагрузку обычно схематизируют. Это приводит к довольно громоздким выкладкам. Поэтому частное решение целесообразно строить так, чтобы оно давало непрерывные значения § и MI на границах участков. В этом случае условия совместности деформаций будут выполняться автоматически, и постоянные С, и С2 будут иметь единые значения для всей пластины. [31]
При этом расчет пластины сводится к решению двух не связанных друг с другом задач - изгибу пластины под действием только поперечных нагрузок и обобщенному плоскому напряженному состоянию. [32]
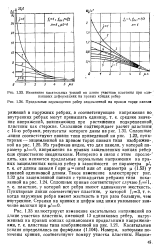 |
Изменение касательных усилий по длине участков пластины при оди наковых деформациях на правых концах ребер.| Продольные перемещения ребер защемленной на правом торце панели. [33] |
Сказанное подтверждает расчет пластины с 14 - ю ребрами, результаты которого даны на рис. 1.31. Сплошные линии соответствуют панели типа приведенной на рис. 1.22, пунктирные-защемленной на правом торце панели типа изображен -, ной на рис. 1.25. Из графиков видно, что для панели, у которой параметр ц / 6, напряжения на правых защемленных концах ребер еще существенно неодинаковы. [34]
 |
Пластины. пластин и образования сфероидаль. [35] |
В основу расчета пластин была положена формула проф. [36]
Изложенная методика расчета пластин с ребрами применима также при одностороннем расположении ребер, при условии, что жесткость пластины на растяжение велика по сравнению с жесткостью на растяжение ребер. В этом случае можно приближенно считать, что сечение ребра поворачивается относительно центра, расположенного на срединной плоскости пластины. [37]
Рассмотрим особенности расчета пластин -, у которых толщина плавно изменяется по радиусу. [38]
 |
Предохранительные пластины. а - с канавкой. б - без канавки.| Устройство для установки предохранительных пластин. [39] |
В основу расчета пластин была положена формула проф. [40]
В задачах расчета пластин вариационные методы позволяют получить приближенное выражение для прогиба пластины с точностью, достаточной для инженерной практики. При этом искомая функция прогиба задается в виде аналитического выражения, соответствующего характеру изогнутой срединной поверхности пластины и удовлетворяющего граничным условиям. Это выражение должно содержать неизвестные коэффициенты или функции одной переменной, для определения которых используется один из вариационных принципов. Такой подход позволяет свести задачу интегрирования дифференциального уравнения в частных производных, описывающего изгиб пластины, к решению системы линейных алгебраических уравнений или системы обыкновенных дифференциальных уравнений. [41]
Рассмотрим пример расчета пластин с несколькими участками с помощью изложенного метода. [42]
Задача о расчете пластин с прямоугольным очертанием контура оказывается значительно более сложной, чем симметричных круглых пластин. Для прямоугольной пластины ( рис. 10.28) в качестве таких переменных берут обычно х и у в прямоугольной системе координат. Дифференциальное уравнение некруглой пластины является уравнением в частных производных и решается, как правило, в рядах. [43]
Задача о расчете пластин с прямоугольным - 3 очертанием контура оказывается значительно более сложной, чем симметричных круглых пластин. Получается это, прежде всего, потому, что прогибы и напряжения несимметричной пластины определяются в функции не одного, а двух независимых переменных. Для прямоугольной пластины ( рис. 351) в качестве таких переменных берутся обычно величины х к у в прямоугольной системе координат. Дифференциальное уравнение некруглой пластины является уравнением в частных производных и решается, как правило, в рядах. [44]
К ним относятся расчет пластин и тонкостенных оболочек с учетом краевого эффекта, изгиб и кручение тонкостенных стержней, определение местных напряжений, расчет элементов конструкций при нелинейных зависимостях между напряжениями и деформациями, ползучесть и релаксация. [45]
Страницы: 1 2 3 4