Расчет - поля - температура
Cтраница 2
При исследовании нестационарного тепломассопереноса в условиях неравномерного поля тепловыделения в сечении пучка и определении эффективных коэффициентов турбулентной диффузии используется модель течения гомогенизированной среды, которая заменяет реальный пучок витых труб и хорошо себя зарекомендовала при расчете стационарных полей температур. Гомогенизированная среда состоит из теплоносителя и твердой фазы. [16]
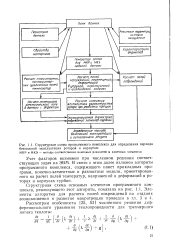 |
Структурная схема программного комплекса для определения периода. [17] |
Учет факторов возможен при численном решении соответствующих задач на ЭВМ. В связи с этим далее изложен алгоритм программного комплекса, содержащего пакет прикладных программ, конечно-элементные и разностные модели, ориентированного на расчет полей температур, напряжений и деформаций в роторах и корпусах турбин. [18]
Изучение особенностей работы твердотельного лазера, связанных с его термооптикой, требует знания процессов преобразования подводимой к лазеру энергии и закономерностей формирования тепловых полей в лазерных активных элементах. Решения задач по определению распределения энергии по различных каналам ее преобразования и тепловых полей в элементах излучателя конкретного лазера сложны и должны проводиться для каждой системы в отдельности. Ниже приводятся характерные для промышленных неодимовых лазеров составляющие энергетического баланса излучателя и формулы для расчета полей температуры, напряжений и деформаций в активных элементах наиболее типичных форм. Эти сведения могут быть полезными для инженеров-разработчиков при проведении оценочных расчетов. [19]
При этом угол закрутки оси струи был равен углу закрутки витых труб на соответствующем радиусе пучка. Поэтому экспериментально определяемый коэффициент Dt в этом случае не учитывает влияние закрутки потока закрученным пучком в азимутальном направлении и его можно сравнивать с коэффициентом Dt для прямого пучка витых труб, что позволяет выявить эффекты, присущие течению в закрученном пучке, на тепломассоперенос в нем. В то же время эффект закрутки потока закрученным пучком на азимутальный перенос может быть учтен введением в уравнения движения и энергии, используемые для расчета полей температур и скоростей в пучке, членов, ответственных за конвективный организованный перенос в азимутальном направлении, обусловленный закруткой пучка витых труб относительно его оси по заданному закону. [20]
Как уже отмечалось, теплообменный аппарат с закрученным пучком витых труб позволяет обеспечить более равномерное поле температур в поперечном сечении пучка при азимутальной неравномерности подвода тепла благодаря дополнительному механизму переноса путем закрутки потока теплоносителя относительно оси пучка по сравнению с прямым пучком витых труб. При этом происходит интенсификация теплообмена в пучке и несколько повышаются гидравлические потери в межтрубном пространстве аппарата. Интенсивное выравнивание неравномерностей поля температур в поперечном сечении пучка повышает надежность работы теплообменного аппарата, а интенсификация теплообмена улучшает его массо-габаритные характеристики. Для расчета полей температур в закрученных пучках требуется изучить процесс тепломассо-переноса и определить эффективный коэффициент турбулентной диффузии Dt, или безразмерный коэффициент К3, определяемый по (4.3) и используемый для замыкания системы дифференциальных уравнений, описывающих течение в пучке. [21]
Метод конечных разностей основан на замене производных их приближенным значением, выраженным через разности значений функции в отдельных дискретных точках - узлах сетки. Дифференциальное уравнение в результате таких преобразований заменяется эквивалентным соотношением в конечных разностях, решение которого сводится к выполнению несложных алгебраических операций. Окончательный результат решения дается выражением, по которому значение будущего потенциала ( температуры) в данной точке ( узле) является функцией времени, ее настоящего потенциала и настоящего потенциала смежных узловых точек. Повторяемость одинаковых операций при расчете полей температуры создает большие удобства для применения современной вычислительной техники, благодаря чему эффективность работы во много раз увеличивается. [22]
Заседателева [28] установлен ряд важных особенностей тепло - и массопереноса в бетоне сооружений в стадии их эксплуатации. Процессы влагопереноса в затвердевшем бетоне имеют существенные различия в двух температурных диапазонах - при температурах нагрева до 100 С и при температурах нагрева выше ЮДОС. В первом температурном диапазоне основной причиной влагопереноса является градиент потенциала массопереноса. При этом считается возможным процессы тепло - и массопереноса рассматривать раздельно, так как распределение температур в бетоне стабилизируется намного быстрее, чем распределение влажности. Это позволяет существенно упростить расчет полей температуры и влажности. Во втором температурном диапазоне перенос обусловлен в основном градиентом нерелаксируемого давления пара в бетоне. Процесс влагопереноса осуществляется, по мнению авторов работы [28], углублением фронта испарения внутрь бетона. В этом случае также возникает возможность существенно упростить аналитическое описание тепло - и массообмена, рассматривая два сопряженных температурных поля с подвижной границей раздела - фронтом испарения. При этом учитывается влияние влажности бетона на коэффициент температуропроводности и возможность фазовых переходов воды в бетоне в лед при температурах ниже 0 С. [23]
Страницы: 1 2