Расчет - оптимальная программа
Cтраница 1
Расчет оптимальной программы является лишь одной из задач, связанных с управлением установкой термического крекинга. [1]
Методы расчета оптимальных программ также принято разделять на два класса. К первому относятся прямые методы, которые используют тот или иной способ редукции вариационной задачи (4.1) - (4.3) к конечномерной задаче. [2]
Методы расчета оптимальных программ принято разделять на два класса. К первому относятся прямые методы, которые используют тот или иной способ редукции ( сведения сложного к более простому) вариационной задачи (8.3.1) - (8.3.4) к конечномерной задаче математического программирования. Ко второму классу относятся методы, использующие необходимые условия. Эта классификация достаточно условна, так как при решении конкретных задач оба класса методов часто дополняют друг друга, тем не менее она удобна, поскольку показывает существенное различие в подходах к решению рассматриваемых задач. [3]
Методы расчета оптимальных программ также принято разделять на два класса. К первому относятся прямые методы, которые используют тот или иной способ редукции вариационной задачи (4.1) - (4.3) к конечномерной задаче. [4]
Обширный класс методов расчета оптимальных программ доставляют методы, опирающиеся на необходимые условия оптимальности. [5]
Существует класс задач расчета оптимальных программ, для которых могут быть предложены эффективные регулярные способы решения. Для таких задач отыскание оптимальной программы сводится к решению задачи Коши без дополнительных процедур отыскания корней функции, как это было в предыдущем пункте. [6]
В теории численных методов расчета оптимальных программ особую роль играет - принцип максимума. [7]
В теории численных методов расчета оптимальных программ особую роль играет принцип максимума. [8]
В настоящее время методы расчета оптимальных программ, использующие необходимые условия в форме принципа максимума - Понтрягина, превратились в большую самостоятельную-главу вычислительной математики. В этом параграфе мы ограничились схематичным изложением лишь некоторых идей, ил люстрирующих основные направления, по которым развиваются эти методы. [9]
Кроме того, при решении задачи расчета оптимальной программы мы обычно используем вместо уравнений (5.1) некоторое упрощенное описание: это дает нам возможность относительно просто провести необходимые расчеты. Подобные упрощения глубоко мотивированы - мы об этом уже говорили и еще не раз будем говорить. [10]
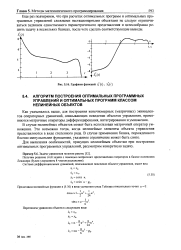 |
Графики функций х ( /, х 2 ( /. [11] |
Еще раз подчеркнем, что при расчетах оптимальных программ и оптимальных программных управлений сложными нестационарными объектами не следует ограничиваться заданием единственного параметрического представления и целесообразно решить задачу в нескольких базисах, после чего сделать соответствующие выводы. [12]
Этот факт накладывает определенные ограничения на использование численных методов расчета оптимальных программ. Как мы увидим ниже, форма записи справа налево удобна при реализации метода Крылова - Чер-ноусько. [13]
Таким образом, в самом общем случае квадратичного функционала задача расчета оптимальной программы для линейной системы сводится к краевой задаче для системы линейных дифференциальных уравнений. [14]
Таким образом, в самом общем случае квад-ратичного функционала, задача расчета оптимальной программы для линейной системы сводится к краевой задаче для системы линейных дифференциальных уравнений. [15]
Страницы: 1 2