Расчет - фазовое равновесие
Cтраница 3
Для реальных растворов расчеты фазового равновесия с использованием коэффициента активности не достаточно точны даже для ограниченного числа систем, поэтому для построения кривых равновесия приходится частично использовать экспериментальные данные. [31]
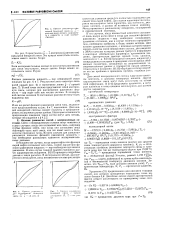 |
Кривая равновесия идеальной бинарной смеси ( х, у - мольные доли легкого компонента в жидкости и паре соответственно.| Крива я равновесия бинарной смеси с томкоЛ азеотраиии ( v, . / - 5. [32] |
И все же расчет фазового равновесия смеси типа, аналогичного представленному на рис. 6 и 7, невозможен. Для каждой конкретной системы следует получить и проанализировать экспериментальные данные. [33]
При многократном проведении расчетов фазовых равновесий использование ЭВМ представляется совершенно необходимым. В книге по мере изложения материала приведено много коротких программ, в том числе предназначенных для решения задач и рассматриваемых в книге примеров. [34]
Прогресс в методах расчета фазовых равновесий, наблюдающийся с середины 60 - х гг., в значительной мере связан с появлением нового типа уравнений для gE и YJ, за которыми закрепилось общее название - уравнения ( модели) локального состава. При их выводе существенную роль, как это следует из названия, играет представление о локальном, микроскопическом составе раствора. [35]
Представленные выше результаты расчета фазовых равновесий жидкость-жидкость по модели UNIFAC с параметрами, оцененными из данных о равновесиях жидкость-пар, могут быть кратко подытожены следующим образом. Хорошие результаты получаются для систем типа II с большими областями расслаивания. Расчет оказывается менее точным, когда в системах типа II область расслаивания невелика. Для большинства систем типа I расчет дает качественно верные результаты, однако, во всех системах вблизи критической точки наблюдается плохое согласие расчета с экспериментом. [36]
При многократном проведевля расчетов фазовых равновесий использование ЭВИ представляется совершенно необходимым. [37]
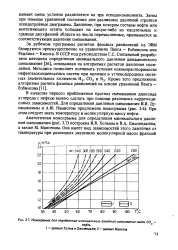 |
Номограмма для определения минимального давления смешивания смеси СО. [38] |
За рубежом программы расчетов фазовых равновесий на ЭВМ базируются преимущественно на уравнениях Пенга - Робинсона или Редлиха - Квонга. В СССР под руководством Г.С. Степановой разработана методика определения минимального давления динамического смешивания [36], основанная на алгоритмах расчетов давления схождения. [39]
При многократном проведении расчетов фазовых равновесий использование ЭВМ представляется совершенно необходимым. В книге по мере изложения материала приведено много коротких программ, в том числе предназначенных для решения задач и рассматриваемых в книге примеров. [40]
Например, задача расчета фазового равновесия N - компонентной смеси является определенной, если заданы рабочие давление и температура, а также мольные концентрации ( N - lj компонентов в смеси. [41]
Ключевой проблемой в расчете многокомпонентного фазового равновесия служит отыскание выражения шя. [42]
За последние годы для расчета фазовых равновесий в многокомпонентных водно-солевых системах широко используется метод Питцера ( Pitzer К. [43]
На основе описанного метода расчета фазового равновесия разработан простой численный алгоритм поиска критической точки. Он основывается на минимизации длины ноды, определенной как сумма модулей разности значений составов / - го компонента в первой и второй фазах. [44]
Другой широко используемый метод расчета фазовых равновесий основан на использовании понятия давления схождения с использованием данного из атласа NGAA. [45]
Страницы: 1 2 3 4