Расчет - стержневая система
Cтраница 3
Традиционные методы расчета стержневых систем имеют такую же последовательность, и многие ее аспекты подробно исследованы при разработке математического обеспечения для стержневых систем. Однако приложение этой схемы к расчету двумерных и трехмерных объектов требует решения многих специальных ъопросов. Одним из них является назначение расчетных узлов. Для стержневых систем эта процедура никаких затруднений не вызывает. Для двумерных и трехмерных объектов эта процедура сходна с процедурой нанесения расчетной сетки в других численных методах. Положение часто осложняется высоким градиентом разрешающей функции, что вызывает необходимость сгущения расчетной сетки. По-видимому, автоматизация этого процесса будет весьма затруднительной, хотя за рубежом уже имеются примеры автоматического построения расчетной сетки для простейших случаев. [31]
Изучение раздела курса Расчет стержневых систем с использованием ЭВМ может быть эффективным только в том случае, если студенты в процессе обучения составят простейший программный комплекс. До изучения курса строительной механики студенты изучают курс Алгоритмические языки и программирование. Изучение программирования проводится на примерах. [32]
Таким образом алгоритм расчета стержневых систем при ударном нагружении заключается либо в непосредственном использовании закона сохранения энергии (12.3), либо в следующей последовательности действий. [33]
Сущность предлагаемого метода расчета стержневых систем с неподвижными узлами поясним на простом конкретном примере. Попутно введем также основные понятия и определения, которыми будем пользоваться в дальнейшем изложении. Пусть требуется рассчитать систему, изображенную на фиг. Узлы системы условимся обозначать одной цифрой, стержни - двумя цифрами. [34]
Существует много методов расчета стержневых систем на устойчивость: метод перемещений, метод сил, метод фокусов, метод начальных параметров и др. Наиболее эффективным из всех этих методов является метод перемещений. [35]
Итак, при расчете стержневой системы сначала находится конечное множество величин ( концевые усилия и ( или) перемещения), зная которые без затруднений можно найти континуальную информацию о напряженно-деформированном состоянии всех стержней системы. В силу конечности множества неизвестных, определяемых в первую очередь, и дискретности расположения сечений, к которым они относятся, стержневые системы могут быть названы дискретными. Хотя, строго говоря, при полном объеме решения проблемы после отыскания дискретной информации ищутся функции, описывающие напряженно-деформированное состояние континуально. [36]
В девятой главе рассмотрен расчет стержневых систем с использованием ЭВМ. Для лучшего понимания расчета на ЭВМ первоначально рекомендуется провести ряд расчетов на калькуляторах. Широкое использование калькуляторов и их доступность позволяют л чше и быстрее понять работу программы на ЭВМ. Далее показано, что наиболее удобным методом расчета стержневых систем на ЭВМ является метод перемещений. [37]
Гордеев а, К расчету стержневых систем на резонанс с помощью ЭВМ, Сб. [38]
Прежде чем переходить к расчету стержневых систем на ЭВМ, рекомендуется провести ряд расчетов с использованием калькуляторов. Любой калькулятор имеет либо запоминающий регистр, либо ячейку памяти. [39]
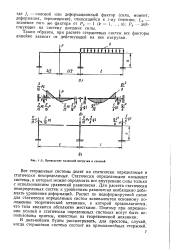 |
Приведение заданной нагрузки к узловой. [40] |
Таким образом, при расчете стержневых систем все факторы линейно зависят от действующей на нее нагрузки. [41]
В предыдущем параграфе при расчете стержневых систем использовался метод Ньютона - Рафсона. Этот метод позволяет найти равновесное положение системы. Но при этом неясно, является ли найденное положение устойчивым или неустойчивым. Для того чтобы ответить на этот вопрос, необходимо проанализировать касательную матрицу жесткости. Если эта матрица для равновесного положения является положительно определенной, то найденное положение равновесия является устойчивым. [42]
В главе 3 приведены методы расчета стержневых систем, балок, рам и некоторых типов тонкостенных элементов из композиционных материалов. Дан обзор и анализ современного состояния строительной механики, основных концепций и методов расчета. Рассмотрены задачи статики, динамики и устойчивости. Отмечены особенности области применения и пути дальнейшего совершенствования используемых методов. Рассматриваемые вопросы иллюстрированы примерами. [43]
В качестве конечных элементов для расчета стержневых систем используются прямолинейные стержни с жестким защемлением концов или шарнирным оттиранием и жесткой заделкой. [44]
В главе 3 приведены методы расчета стержневых систем, балок, рам и некоторых типов тонкостенных элементов из композиционных материалов. Дан обзор и анализ современного состояния строительной механики, основных концепций и методов расчета. Рассмотрены задачи статики, динамики и устойчивости. Отмечены особенности области применения и пути дальнейшего совершенствования используемых методов. Рассматриваемые вопросы иллюстрированы примерами. [45]
Страницы: 1 2 3 4