Расчет - критическая скорость
Cтраница 1
Расчет критической скорости ( или частоты собственных колебаний) вала переменного сечения, несущего ряд масс, производится следующим образом. [1]
Поэтому расчет критической скорости разрушения без учета влияния этих моментов дает оценку сверху для точного значения этой скорости. [2]
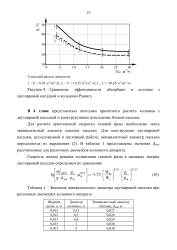
Метод расчета критической скорости псевдоожижения, предложенный в работе [3], основывается на эталонной зависимости коэффициента трения от критерия Рейнольдса, которую авторы получили для частиц сферической формы. [3]
Для расчета критических скоростей вала на двух жестких опорах с успехом применяется также метод, предложенный В. М. Фридманом [68] и сочетающий высокую точность с простотой вычислений. [4]
 |
Значения эквивалентного диаметра двутавровой насадки при различных диаметрах колонного аппарата. [5] |
Для расчета критической скорости газовой фазы необходимо знать эквивалентный диаметр каналов насадки. В таблице 1 представлены значения d3KB, рассчитанные для различных диаметров колонного аппарата. [6]
При расчете критических скоростей, как отмечалось в десятой главе, ротор турбогенератора рассматривают как балку переменного сечения на двух шарнирных опорах. Деформациями от перерезывающих сил и моментами сил инерции масс пренебрегают, а податливые изотропные опоры вала считают расположенными на оси подшипников. [7]
При расчете критической скорости ротора электрошпинделя на воздушных опорах ротор рассматривается как незакрепленная свободная балка. [8]
Аналитические способы расчета критических скоростей могут использоваться только для простейших расчетных схем, когда вал имеет постоянное сечение, когда можно пренебречь влиянием массы вала на критическую скорость ротора, когда число сосредоточенных на валу нагрузок меньше трех - четырех. Иначе эти способы становятся чрезвычайно сложными и громоздкими в реализации, либо появляются значительные расхождения между реальной конструкцией ротора и его расчетной схемой, что делает сомнительными результаты расчета. Для приблизительной оценки первой критической скорости многомассовых роторов разработан ряд приближенных методов расчета. Рассмотрим некоторые из них. [9]
При решении задачи расчета критических скоростей установки этот корень соответствует наиболее важному и опасному явлению прямой прецессии, когда направление вращения изогнутой оси вала совпадает с направлением его собственного вращения. Обратная прецессия, соответствующая первому корню уравнения, в реальных установках, как правило, не наблюдается и во всяком случае не достигает такого опасного развития. При расчете колебаний, вызываемых гидродинамическими усилиями на гребном винте, эта частота также играет определяющую роль, поскольку соответствует максимальному развитию колебаний в плоскости действия возбуждения - в вертикальной плоскости, где система жестче и податливости меньше. [10]
В данном разделе рассмотрен расчет критической скорости ротора в - случае прямой синхронной прецессии, когда оба вращательных движения совпадают по величине и направлению. В раде случаев может иметь место и обратная прецессия, когда собственно вращение и прецессия противоположны по направлению. [11]
Эта формула пригодна для расчета критической скорости шин с высоким внутренним давлением. [12]
Фридман, Аналитический метод расчета критических скоростей вращения валов, сб. [13]
Податливость опор В большинстве случаев расчет критической скорости вращения производят в предположении, что опоры являются абсолютно жесткими. [14]
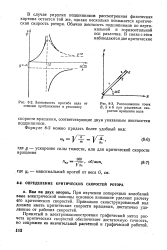 |
Зависимость прогиба вала от степени приближения к резонансу.| Расположение точек В, S и G при различных скоростях вращения вала. [15] |
Страницы: 1 2 3 4