Расчет - упругая характеристика
Cтраница 1
Расчет упругих характеристик с помощью импульсного акустического метода проводится по формулам, в которых необходимо учитывать структуру материала обшивок и пенопласта. В качестве обшивок трехслойных конструкций используются алюминий, асбестоцемент, древеснослоистые пластики, древесностружечные плиты, фанера, стеклопластики и другие материалы. [1]
Расчет упругих характеристик элементарного слоя содержит два этапа: определение характеристик приведенной матрицы за счет усреднения упругих свойств волокон, уложенных в направлении, перпендикулярном к плоскости слоя, со связующим; и расчет характеристик слоя исходя из упругих свойств волокон, параллельных плоскости слоя, и свойств модифицированной матрицы. Таким образом, последующий расчет деформативных характеристик слоистого материала определяется выбором направлений армирования, которые усредняются при модификации свойств матрицы или являются арматурой выделенного элементарного слоя. [2]
Расчет упругих характеристик диафраг-менных нажимных устройств автотракторных сцеплений вдавливаемого и вытягиваемого типов / / Изв. [3]
Для расчета упругих характеристик используются средние значения скоростей распространения ультразвуковых волн в полимерных материалах при различных давлениях. [4]
 |
Схема разбиения на слои материала, образованного системой двух нитей. а - расположение волокон в материале. б - расположение волокон в смежных слоях. [5] |
Для расчета упругих характеристик ( постоянных) слоя ( см. рис. 9.2) используют два подхода. Подход заключается в определении, во-первых, характеристик анизотропного связующего - модифицированной матрицы, во-вторых, свойств однонаправленного слоя с модифицированной матрицей. Последняя получается усреднением ( в этом и состоит принцип частичного сглаживания) арматуры, расположенной ортогонально по отношению к слою, со связующим. Плоскость изотропии приведенной матрицы совпадает с плоскостью слоя. [6]
При расчете упругих характеристик предполагалось, что нитевидные кристаллы хаотически располагаются во всем объеме матрицы. Принятое расположение близко к реальному расположению в материале при вискериза-ции как из аэрозоля и суспензии, так и из газовой фазы. Справедливость такого предположения подтверждается удовлетворительным совпадением экспериментальных и расчетных значений упругих постоянных. [7]
При расчете упругих характеристик волокнистых композиционных материалов выделяется типичный объем. Он состоит из заданного числа волокон, распределенных в матрице ( с указанием расстояний и угловых смещений) так, чтобы упаковка армирующих волокон по всему объему материала была идентичной их размещению в типичном объеме. Если определено напряженно-деформированное состояние во всех компонентах, входящих в типичный объем, то эффективными или приведенными упругими характеристиками композиционного материала являются коэффициенты, связывающие усредненные по типичному объему компоненты напряжений и деформаций. [8]
Данный метод расчета упругих характеристик не исключает многозначности полученных оценок. Дело в том, что плоскость армирования ij, параллельно которой выполняется условное деление композиционного материала на слои, может быть перпендикулярна любому из трех направлений армирования. При этом расхождение в значениях упругих констант, рассчитанных для направлений, параллельных плоскости слоя, как это будет показано в дальнейшем, незначительно, и им можно пренебречь. [9]
В основу расчета упругих характеристик для всех исследованных материалов положен принцип суммирования повторяющихся элементарных слоев, содержащих волокна двух направлений. Для расчета упругих характеристик элементарного слоя использованы два подхода [1-4, 49], которые при расчете модулей Юнга в направлении армирования и коэффициентов Пуассона в плоскости слоя дают идентичные результаты. При этом, как и в работах [1, 49], для модулей сдвига используются формулы [10, 86], полученные на основе регулярных моделей однонаправленного материала. Модуль упругости в направлении армирования EI малочувствителен к способу расчета: все методы дают близкие результаты. Кроме того, расчетные зависимости для указанных констант весьма просты и удобны для практических вычислений. [10]
Данный метод расчета упругих характеристик не исключает многозначности полученных оценок. Дело в том, что плоскость армирования ij, параллельно которой выполняется условное деление композиционного материала на слои, может быть перпендикулярна любому из трех направлений армирования. При этом расхождение в значениях упругих констант, рассчитанных для направлений, параллельных плоскости слоя, как это будет показано в дальнейшем, незначительно, и им можно пренебречь. [11]
Например, для расчета упругих характеристик Дисперсно наполненного полимера, в котором частицы наполнителя распределены в матрице случайным, хаотическим образом, обычно используют модели регулярной структуры. Однако, как показывают экспериментальные исследования, приведенные на моделях, регулярные структуры не всегда могут отразить не только количественно упругие характеристики такого композита, но и качественные особенности измерения этих характеристик с хаотическим распределением наполнителя ( в отличие от регулярного) обнаруживаются так называемые перколяционные эффекты. [12]
Принятые допущения существенно упрощают расчет упругих характеристик деформационной модели, внося при этом следующие особенности. [13]
Это позволяет использовать для расчета упругих характеристик разработанную для упругих материалов теорию армированных сред. [14]
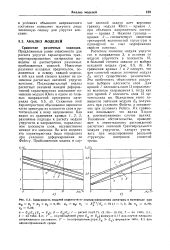 |
Зависимость модулей упругости от перераспределения арматуры в материале при И2 Ц ] Ц2 Д3 0 45. ц, Ц2. nf. / ЕС 25 ( i - 1, 2, 3. va 0 20. [15] |
Страницы: 1 2 3