Расчет - упругая характеристика
Cтраница 2
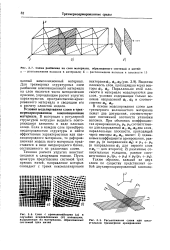
Предложенные ранее зависимости для расчета упругих характеристик трех-мерноармированных материалов выведены из рассмотрения различных приближенных моделей. Известные различия исходных предпосылок, положенных в основу каждой модели, в той или иной степени влияют на изменение расчетных значений упругих констант. Снижение этой характеристики обусловлено переносом части арматуры из плоскости слоя в ортогональное к нему направление. Во всех моделях эта характеристика была определена при условиях деформирования по Фойггу. [16]
Анализ изложенных подходов к расчету упругих характеристик композиционного материала показывает, что наиболее корректный учет сближения волокон и влияния схемы укладки арматуры на эффективные характеристики материала возможен на уровне решений граничных задач теории упругости для многосвязной области. Такой подход очень громоздок и связан с трудоемким численным анализом. [17]
Возможность использования зависимостей (4.13) - (4.19) при расчете упругих характеристик материалов, образованных системой двух нитей, оценивалась на различных типах стеклопластиков, структурные схемы армирования которых были показаны на рис. 4.3, У исследованных материалов в широких пределах варьировался угол наклона волокон основы к оси х, объам-аое содержание и свойства армирующих волокон. [18]
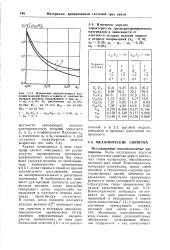 |
Изменение относительных значений модулей Юнга и сдвига от плотности укладки волокон направления 3 при, а2 0 10. Ег рассчитано по, . E I - по. 02з - по. GM - по. [19] |
Анализ приведенных в этом параграфе данных показывает, что расчет упругих характеристик трехмерно-армированных материалов без учета шага укладки волокон по приближенным зависимостям, приведенным в § 5.1, может явиться одной из причин значительного расхождения между их экспериментальными и расчетными значениями. В особенности это имеет место для высокой плотности распределения волокон, когда прослойка связующего вдоль какого-либо направления в плоскости сечения материала практически отсутствует. [20]
Как и для двух последних групп материалов, он включает в себя расчет упругих характеристик модифицированной матрицы и расчет характеристик композиционного материала с учетом свойств модифицированной матрицы. [21]
Как было показано выше, основным параметром, входящим в формулы для расчета упругих характеристик, является скорость распространения упругих волн. [22]
Для трехмерных структурных схем разбиение композиционного материала на слои является чисто методическим приемом, упрощающим расчет упругих характеристик пространственно-армированного материала и сводящим его к расчету слоистой модели. [24]
Простые модели существуют и для однонаправленного волокнистого материала, для которого разработаны достаточно точные методы расчета упругих характеристик. Для обоих слоев расчет дает приближенные характеристики материала. [25]
Расчет упругих характеристик рассматриваемого типа материалов проводили путем сведения реальной их структуры к слоистой модели, как это изложено на с. [26]
В основу расчета упругих характеристик для всех исследованных материалов положен принцип суммирования повторяющихся элементарных слоев, содержащих волокна двух направлений. Для расчета упругих характеристик элементарного слоя использованы два подхода [1-4, 49], которые при расчете модулей Юнга в направлении армирования и коэффициентов Пуассона в плоскости слоя дают идентичные результаты. При этом, как и в работах [1, 49], для модулей сдвига используются формулы [10, 86], полученные на основе регулярных моделей однонаправленного материала. Модуль упругости в направлении армирования EI малочувствителен к способу расчета: все методы дают близкие результаты. Кроме того, расчетные зависимости для указанных констант весьма просты и удобны для практических вычислений. [27]
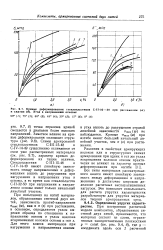 |
Кривые деформирования стеклопластиков С-П-32 - 50 при растяжении ( а и сжатии ( б. Угол к направлению основы. [28] |
Все типы материалов рассматриваемого класса имеют линейную зависимость между деформациями и напряжениями в достаточно широком диапазоне расчетных эксплуатационных нагрузок. Это позволяет использовать для расчета упругих характеристик разработанную для упругих материалов теорию армированных сред. [29]
Рассмотренные ранее приближенные методы расчета упругих характеристик слоя нетрудно распространить на вычисление констант трехмер-ноармированного композиционного материала. [30]
Страницы: 1 2 3