Расчет - частота - колебание
Cтраница 2
Первый вопрос, который при этом возникает, - это расчет частот колебаний. Решение этого вопроса возможно осуществить методами классической механики, и какие-либо трудности принципиального характера здесь не возникают. [16]
В упомянутых работах было показано, что обычный электростатический метод расчета частот колебаний решетки ионных кристаллов непригоден в тех случаях, когда речь идет о непродольных дипольных колебаниях с фазовой скоростью vpE ( q) / %, большей скорости света в среде. В дальнейшем выяснилось, что этот вывод является справедливым также и для области спектра экситонов. [17]
Вместо прежних неудовлетворительных методов расчета частот колебаний многоатомных молекул М. А. Ельяшевичем и Б. И. Степановым были разработаны общие методы расчета частот колебаний, учитывающие специфику строения молекул и позволяющие максимально упростить решение задачи и стандартизовать методику решения. При помощи этих методов удается рассчитывать колебания очень сложных молекул, насчитывающих десятки атомов, и определять системы силовых постоянных, реально характеризующие классы сходных молекул и позволяющие предсказывать колебательные спектры соединений, не изученных экспериментально. [18]
Прежде чем перейти к изложению полученных результатов, остановимся коротко на описании используемых в работе методов расчета частоты решеточных колебаний. [19]
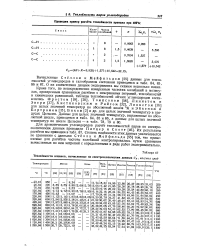 |
Теплоемкости алканов, вычисленные по спектроскопическим данным Ср, кал / мол град. [20] |
Степень надежности этих данных увеличивается по сравнению с данными Стелла и Мейфильда [55] тем, что применяемые для расчетов частоты колебаний контролировались путем сравнения вычисленных по ним энтропии с определенными в ряде работ экспериментально. [21]
Выявление характеристических структурных элементов с присущей им совокупностью характеристических линий требует, наряду с экспериментальным изучением и сопоставлением спектров ряда близких соединений, также проведения расчетов частот колебаний простейших молекул, обладающих данным характеристическим структурным элементом. [22]
Для точного расчета требуется тщательное изучение спектра вещества ( как спектра комбинационного рассеяния, так и ИК-спектра), детальное и однозначное толкование всех линий спектра, распределение их в серии; подыскание формул для расчета частот колебаний и, наконец, что является труднейшей задачей, разрешаемой с помощью методов статистической механики, нахождение статистических весов уровней. Кроме того, необходим учет взаимного влияния различных энергетических уровней. [23]
Для точного расчета требуется тщательное изучение спектра вещества ( как по методу комбинационного рассеяния, так и в инфракрасной области), детальное и однозначное толкование всех линий спектра, распределение их в серии; подыскание формул для расчета частот колебаний и, наконец, - что является труднейшей задачей, разрешаемой с помощью методов статистической механики, - нахождение статистических весов уровней. Кроме того, необходим учет взаимного влияния различных энергетических уровней. [24]
Такая конструкция подшипниковых узлов позволяет уменьшить частоту собственных колебаний системы, которая работает в закритической области. Расчет частоты колебаний с упругими подшипниками приведен в гл. [25]
Такая конструкция подшипниковых узлов позволяет уменьшить частоту собственных колебаний системы, которая работает в закритической области. Расчет частоты колебаний вала с упругими подшипниками приведен в гл. Для смазывания винтовой передачи распыляется масло, залитое в картер привода. [26]
Частоты колебаний гармонического осциллятора, предсказываемые классической и квантовомеханической теориями, совпадают. Задача расчета частот колебаний исходя из заданной геометрии системы и численных значений констант, равно как и обратная задача, решаются методами классической механики. Однако определение силовых констант исходя из значений частот нормальных колебаний системы представляет для квантовой механики неизмеримо более трудную проблему. [27]
Частоты колебаний гармонического осциллятора, предсказываемые классической и квантовомеханической теориями, совпадают. Задача расчета частот колебаний исходя из заданной геометрии системы и численных значений констант, равно как и обратная задача, решаются методами классической механики. Так, Вильсон 167 приводит решения этих задач, выполненные матричным методом. Однако определение силовых констант исходя из значений частот нормальных колебаний системы представляет для квантовой механики неизмеримо более трудную проблему. [28]
 |
Примеры применения правила изотопного сдвига ( уравнение. [29] |
Уравнение (5.16) наглядно показывает, что частота изменяется тем меньше, чем больше вклад необмененных атомов в энергию соответствующего колебания. В [925] уравнение (5.16) использовали для расчета частот колебаний Н2О, NH3 и групп С - Н, - СН2, - СНз - В табл. 5.2 собрана часть полученных результатов. [30]
Страницы: 1 2 3