Значение - медиана
Cтраница 1
Значения медианы показывают, что средняя заработная плата в электронике выше, чем в строительстве. Межквартильный размах дает интервал, содержащий центральные 50 % работников. Для работников строительной отрасли значение размаха больше, что свидетельствует о большей вариации значений заработной платы в данной отрасли. [1]
Значения медианы не могли быть получены аналитически. Но все же взятые из точных таблиц они являются теоретически вполне надежными. [2]
Значение медианы не изменится, если большие значения станут еще больше, а малые - еще меньше. Поэтому медианой пользуются для характеристики данных, в которых имеются редкие, но очень сильные отклонения от преобладающих значений. Например, если один из сотрудников отдела получил Государственную премию, то в качестве представительной характеристики доходов этой группы трудящихся за данный месяц следует выбрать значение медианы. [3]
Определяем значение медианы ( Me) по пересечению интегральной прямой с 50 % - ным значением вероятности. [4]
Определяют значение медианы ( Me) по пересечению интегральной прямой с 50 % - ным значением вероятности. [5]
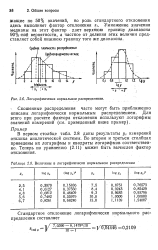 |
Логарифмически нормальное распределение.| Величины в логарифмически нормальном распределении. [6] |
Умножение значения медианы на этот фактор дает верхнюю границу диапазона 90 % - ной вероятности, а частное от деления этих величин представляет собой нижнюю границу того же диапазона. [7]
Для интерполяции значений медианы в тех же пределах значений а на рис. 17 приведен соответствующий график. Далее покажем на примерах, как надо производить обработку измерений в случаях, когда возникает, предположение или имеется уверенность в асимметричном распределении отклонений. [8]
Не умаляя значения медианы в анализе, отметим, что она все же не основная, а дополнительная характеристика совокупности. Основной характеристикой является средняя величина. Лишь при решении некоторых задач, особенно связанных с определением оптимума, совпадающего с вариантом, приходящимся на середину ряда, медиана имеет самостоятельное значение. Медианой целесообразно пользоваться, когда неизвестны границы открытых крайних интервалов вариационного ряда, на которые приходится значительная часть единиц всей совокупности, так как средняя в этих случаях страдает значительной неточностью. [9]
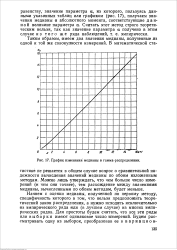 |
График изменения медианы в гамма-распределении. [10] |
Таким образом, имеем два значения медианы, полученные из одной и той же совокупности измерений. [11]
 |
Зоны рассеивания случайных погрешностей. [12] |
Параметр от определяет среднее квадратическое отклонение ряда значений медиан. [13]
Но для полученного значения параметра а л: - 1 12 значение медианы, взятое из табл. 6 приложения I, составляет 12 67, что значительно превышает приведенное выше значение 10 58, взятое непосредственно и. Впрочем, следует помнить, что значение параметра а получено из того же ( короткого) ряда и, следовательно, также содержит ошибку. [14]
Для любого ряда чисел, для любой выборки имеется только одно значение медианы, которое - может быть положительным, отрицательным или равным нулю. [15]
Страницы: 1 2 3