Расширение - базис
Cтраница 2
Симбатное с ц уменьшение АЕ свидетельствует о том, что причиной недооценки устойчивости 2 ыс-конформации 1 2-дифторэтилена является электростатическое отталкивание между двумя атомами фтора. Расширение базиса и включение d - функций, приводящее к равномерному распределению заряда, одновременно увеличивает и относительный вклад стабилизирующего невалентного взаимодействия, на что указывает проведенный в работе [84] анализ за-селенностей перекрывания между атомами F-F. В результате только в расширенном базисе STO-6 - 311G, включающем поляризационные rf - функции, удается качественно верно описать относительную устойчивость цис - и ГуОанс-конформаций 1 2-дифторэтилена. [16]
Расширение базиса позволяет, в частности, учесть то обстоятельство, что основное критическое движение не является, строго говоря, плоским. [17]
К этим трудностям добавляется проблема, с которой мы встретились при попытке расчета энергетических переходов в молекуле водорода, основываясь на неадекватном атомноорбитальном базисе ( см. VI): в общем, возбужденные молекулярные состояния не могут быть описаны достаточно точно с применением волновых функций, построенных только из орбиталей основного состояния составляющих атомов. Расширение атомноорбиталь-ного базиса может значительно улучшить результаты, но не без вычислительных трудностей. [18]
Ясно: чем шире ( полнее) базис АО, тем точнее могут быть найдены самосогласованные МО, однако при этом увеличивается трудоемкость расчета. Расширение базиса АО обычно приводит к понижению вычисленной полной энергии молекулы, но постепенно этот эффект уменьшается по мере того, как энергия приближается к хартри-фоковскому пределу. [19]
Не вдаваясь далее в тонкости расчетных методов, отметим только, что базисные наборы могут быть как Минимальными, так и расширенными, в зависимости от того, включены в них только АО, заполненные в основных состояниях атомов, или же к ним добавлены вакантные АО с более высокими квантовыми числами. Кроме того, расширение базиса может быть связано с увеличением числа функций, аппроксимирующих данную АО. [20]
Не вдаваясь далее в тонкости расчетных методов, отметим только, что базисные наборы могут быть как минимальными, так и расширенными, в зависимости от того, включены в них только АО, заполненные в основных состояниях атомов, или же к ним добавлены вакантные АО с более высокими квантовыми числами. Кроме того, расширение базиса может быть связано с увеличением числа функций, аппроксимирующих данную АО. [21]
 |
Схема молекулярных орбиталей ВеН2. [22] |
Гибридизация по методу МО не обязательна. Ее трактуют просто как расширение базиса АО. Под базисом понимается совокупность близких по энергии АО, принимающих участие в построении МО при образовании молекулы из атомов. Расширение базиса АО состоит в увеличении их числа. При расчета по методу МО с достаточно широким базисом АО нет необходимости специально вводить это понятие. [23]
Йохансен [85] проводил неэмпирические расчеты электронного строения перманганата, МпО4 -, в его основном состоянии Л ], методом МО ЛКАОССП, с использованием в качестве базисных АО гауссовых функций. В этой работе было проведено исследование сходимости результатов неэмпирических расчетов МО перманганата при расширении базиса АО. С этой целью были использованы два различных базисных набора АО, оба достаточно близкие к хартри-фоковско-му пределу для атомов Мп и О. [24]
Из виртуальных МО две ( 2е и 7i 2) являются разрыхляющими, а две другие ( 7а и 8) близки к вакантным 4s - и 4 / 7 - АО металла. Автор [85] особо отмечает то обстоятельство, что вакантные МО lt и 2е располагаются почти вплотную и инвертируют при расширении базиса. Это указывает, что обсуждение электронного спектра MnOJ требует детального расчета возбужденных состояний. [25]
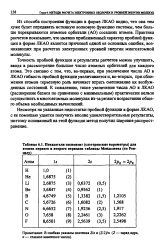
Из табл. 1 видно, что вычисленные значения A-Z. Это объясняется двумя причинами. Во-первых, с расширением базиса вычисляемые значения л мономеров уменьшаются ( приближаясь к истинным значениям), что приводит к уменьшению электростатической части энергии взаимодействия. [26]
Из табл. 1 видно, что вычисленные значения АЕ падают с расширением базиса. Это объясняется двумя причинами. Во-первых, с расширением базиса вычисляемые значения л мономеров уменьшаются ( приближаясь к истинным значениям), что приводит к уменьшению электростатической части энергии взаимодействия. Во-вторых, в расчетах с малыми базисными наборами всегда возникает кажущееся повышение АЕ. Объяснение заключается в том, что при сближении мономеров и объединении их базисных наборов точность расчета энергии мономеров увеличивается, но это не учитывается при определении АЕ. Поскольку этот вычислительный эффект сильнее при меньших R, расчеты с малыми базисными наборами занижают равновесные значения R0 и, следовательно, завышают значения АЕ. [27]
 |
Показателя экснонснт ( слэтеровскве нараметры для атомов первого н второго периодов таблицы Менделеева ( по Реи. [28] |
Это связано с тем, что, во-первых, при увеличении числа АО в ЛКАО гибкость пробной функции увеличивается и, во-вторых, при сближении атомов серьезную роль начинает играть смешивание их возбужденных состояний. К сожалению, такое увеличение числа АО в ЛКАО ( расширение базиса по сравнению с минимальным) практически нельзя осуществить в многоатомных молекулах из-за резкого возрастания общего объема необходимых вычислений. [29]
Чтобы убедиться в том, что данная теорема действительно играет исключительно важную роль, рассмотрим следующую ситуацию. Предположим, что требуется найти решение задачи линейного программирования с 50 линейно независимыми ограничениями и 300 неизвестными. Обратим внимание на то, что увеличение числа линейно независимых ограничений в той или иной модели приводит к расширению базиса. Следовательно, количество переменных, входящих в оптимальное решение, тем больше, чем больше ограничений содержит модель. [30]
Страницы: 1 2 3