Минимальное расширение
Cтраница 1
Минимальное расширение А произвольной булевой алгебры А является полной булевой алгеброй. Канонический изоморфизм / г сохраняет все бесконечные объединения а пересечения. [1]
Теорема, Минимальное расширение существует. [2]
Является ли минимальное расширение отношения г обязательно и пополнением г. Всегда ли пополнение есть минимальное расширение. [3]
Во всяком минимальном расширении & системы Э ( существует такой нормальный делитель 91, что / 91 будет абсолютно минимальным расширением. [4]
Речь идет о минимальном расширении системы программирования ПАРСЕК [11] до сетевой версии, способной обеспечить глобальную програм-мируемость без существенного усложнения процессов программирования. [5]
Эта теорема дает обзор всех неизоморфных минимальных расширений данной системы. Вторая ее часть очевидна. [6]
Мы покажем сейчас, что такое минимальное расширение существует н что оно единственно с точностью до изоморфизма. [7]
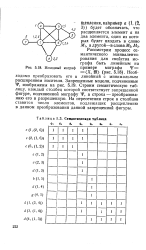 |
Исходный мограф.| Семантическая таблица. [8] |
Необходимо преобразовать его в линейный с минимальным расширением носителя. Строим семантическую таблицу, каждый столбец которой соответствует запрещенной фигуре, подчиненной мографу Т, а строка - преобразованию его в разрешенную. На пересечении строк и столбцов ставится число элементов, подлежащих расщеплению в данном преобразовании данной запрещенной фигуры. [9]
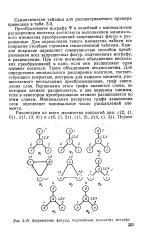 |
Запрещенные фигуры, подчиненные исходному мографу. [10] |
Преобразование мографа 4я в линейный с минимальным расширением носителя достигается выполнением минимального множества преобразований запрещенных фигур в разрешенные. [11]
Если булева алгебра А безатомна, то ее минимальное расширение А также безатомно. [12]
Если булева алгебра Л безатомна, то ее минимальное расширение Л также безатомно. [13]
Мы говорим, что теория умолчаний удовлетворяет свойству единственности минимального расширения, если всякий раз, когда она имеет расширение, у нее существует и минимальное расширение. [14]
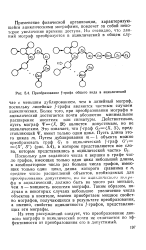 |
Преобразование f - графа общего вида в ациклический. [15] |
Страницы: 1 2 3 4