Рауза
Cтраница 1
 |
Модель Каргина - Слонимского - Рауза ( КСР. [1] |
Рауза, который довел относящиеся к ней расчеты до вычисления практически особо важного случая гармонического нагружения, и называют моделью ожерелья. [2]
Рауза), которая, в свою очередь, испытывает флуктуации в зависимости от времени, и, во-вторых, от положения других бусинок в цепи. [3]
Рауза неприменима при таких малых промежутках времени. [4]
Рауза характерны строгой направленностью. Книга по истории гидравлики знакомит читателя с развитием гидравлических машин, дает представления о гидравлических законах, о первых ирригационных и гидротехнических сооружениях, причем при составлении этой книги были использованы библиотеки многих стран мира. Книга Элементарный курс механики жидкости дает основные представления о жидкости как о физическом континууме и последовательно развивает основные идеи науки о жидкости. Эта книга готовит читателя к чтению и восприятию последующих книг и особенно той, что является предметом предлагаемого перевода, а также до некоторой степени книги Механика жидкости для инженеров-гидротехников, имеющей по замыслу автора прикладной характер. [5]
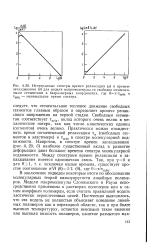
Рауза равен - / 2 и зависимости для всех полимеров, построенные в указанных выше приведенных координатах, совпадают. [6]
Рауза, а значение Н, возрастает с уменьшением молекулярного веса. Качественно это отклонение можно отнести за счет усиления процессов релаксации вследствие увеличения скольжения узлов зацепления, однако точная теория этого явления отсутствует. В действительности ни одна из фракций не является строго однородной и конечные значения времен релаксации не попадают в экспериментальный интервал времени. [7]
При этом предположении Рауз показал, что квазистатическое основное движение устойчиво по отношению ко всем возмущениям этого типа. Доказательство Рауза заключается в следующем. Если какая-либо функция нескольких переменных имеет для определенной системы значении последних минимум х), например f ( х, у) при х х, у у имеет минимальное значение f ( ос, y) - fo, то, выбирая значение функции f ( х, у), достаточно близкое Е f0, можно всегда достигнуть того, что у и х произвольно приблизятся к ж и у. Иначе говоря, если мы хотим добиться того, чтобы ( х - ж) е и ( у - у) е, то при произвольно малом е это может быть достигнуто тем, что в неравенстве f ( х У) - / olTi 1 будет выбрано достаточно малым. [8]
В то время как в 2 мы рассматривали, следуя Раузу, движения, при которых составляющие импульса ujt соответствующие скрытым координатам wjt не менялись со временем, теперь, следуя Леви-Чивита, рассмотрим движения, при которых какие-либо у. [9]
Более адекватной характеристикой гидродинамического поведения макромолекул является модель Картина и Слонимского [57] и Рауза [48, 55], в которой молекулярная цепь представляется в виде совокупности большого числа последовательно ( и свободно) связанных субцепей, каждая из которых представляет собой гауссову цепь свободно-сочлененных сегментов. Такая система характеризуется механическим спектром времен релаксации [57], первый член которого соответствует механическим ( гидродинамическим) свойствам в поле постоянного градиента скорости. [10]
В приближенной теории, являющейся промежуточной между теорией гауссовых субцепей ( модель Каргина-Слонимского - Рауза) и идеальной строгой теорией, за эффективный жесткий элемент может быть принята группа звеньев в цепи, которая в действительности обладает внутренними степенями свободы. [11]
Однако эти и другие данные Рауза и Ситтела и результаты динамических испытаний Мэзона [24], выраженные в трудной для прямого сравнения с теорией форме, так же как последние данные Зимма1), находятся в достаточно хорошем полуколичественном согласии с представлениями Зимма и Рауза. Можно не сомневаться, что эти изменения связаны с кооперативными движениями гибких молекул, как это описывается теориями. [12]
Данные для ряда растворов полиизобутилена и трибутирата целлюлозы приведены па фиг. Рауза в конечной зоне могут быть приписаны гетерогенности молекулярного веса. [13]
Спектры релаксации, показанные на фиг. Рауза, совмещены в конце переходной зоны, соответствующем большим промежуткам времени. [14]
Страницы: 1 2