Кривое реагирование
Cтраница 1
 |
Модель Бертрана. [1] |
Кривые реагирования показывают максимизирующие прибыль размеры выпуска, который будет осуществляться одной фирмой, если даны объемы выпуска фирмы-соперницы. [2]
 |
Кривые реагирования в дуополии Курно. [3] |
Пересечение кривых реагирования двух фирм - точка Е - показывает равновесие Курно: каждая фирма правильно угадывает поведение конкурента и принимает самое оптимальное для себя решение. При равновесии Курно каждый дуополист устанавливает объем производства, который максимизирует его прибыль при данном объеме производства своего конкурента, и поэтому ни у одного дуополиста нет стимула менять свой объем производства. [4]
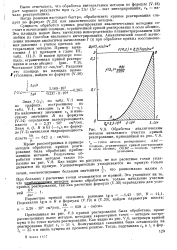 |
Обработка аналитическим методом начального участка кривой реагирования, приведенной на. [5] |
Сущность обработки кривых реагирования аналитическими методами состоит в вычислении площади, ограниченной кривой реагирования и осью абсцисс. Эта площадь может быть вычислена непосредственно планиметрированием или любым из способов численного интегрирования. Аналитический способ вычисления площади аналогичен вычислению / ( t) при обработке кривых восстановления давления с учетом притока интегральным методом. [6]
Методы обработки кривых реагирования при произвольном изменении дебита возмущающей скважины подробно изложены в работе [36] для схемы конечного и бесконечного пластов. Применительно к конечному пласту эти методы кроме параметров пласта позволяют определять его границы и объем. [7]
Для обработки кривых реагирования ( КР) при гидропрослушивании предложен следующий способ. Зависимость, описывающая КР, дважды формально интегрируется: один раз на всем промежутке снятия КР, другой разна интервале на 20 - 30 % меньше первого. Полученные выражения делятся почленно друг на друга, и в результате получается трансцендентное уравнение относительно пье-зопроводности, которое легко решается любым численным методом. После нахождения пьезопроводности вычисляется гидропроводность. При решении трансцендентного уравнения входящие в него интегралы подсчитываются любым методом численного интегрирования. [8]
Методы обработки кривых реагирования по эталонным кривым просты и не требуют продолжительного времени. [9]
На рис. 4 приведены кривые реагирования при гидропрослушивании путем однократного и многократного возмущения. [10]
В статье исследуется влияние на кривые реагирования негерметичности цементного кольца в реагирующей скважине. Предлагается приближенное решение модельной задачи гидропрослуши-вания с учетом перетока газа из одного пласта в другой по негерметичному цементному кольцу. [11]
Когда реакция наступает быстро, обрабатывать кривые реагирования следует по формуле (V.25) пли аналитическим методом. [12]
Рассмотренные в главе VII методы обработки кривых реагирования при произвольном изменении дебита построены на решении уравнения пьезопроводности операционным методом Лапласа. Операционное исчисление в последние годы нашло широкое распро - странение при решении обратных задач подземной гидродинамики и, в частности, задач, связанных с гидродинамическими исследованиями пластов и скважин. Особую ценность операционные методы приобретают при исследовании различных неоднородностей по данным изучения нестационарных процессов в скважинах. [13]
В работе [182] составлена программа обработки кривых реагирования методом подбора по формуле (V.57) на вычислительной машине. [14]
В настоящее время известно несколько методов обработки кривых реагирования, полученных при мгновенном изменении дебита возмущающей скважины на постоянную величину. Под мгновенным изменением дебита возмущающей скважины подразумевается пуск ( если скважина простаивала долгое время) в работу с постоянным дебитом Q или остановка ( если скважина перед этим работала на установившемся режиме) или просто изменение дебита возмущающей скважины на величину Q. Под установившимся режимом в гидропрослушивании понимается существование практически установившегося состояния не только в возмущающей скважине, но и в пласте или в районе возмущающей и реагирующей скважин. [15]
Страницы: 1 2 3