Значение - параметр - уравнение
Cтраница 1
Значения параметров уравнения (2.7), приведенные в табл. 2.5 и 2.6, получены путем стандартной обработки соответствующих изотерм при исследовании кристаллизации полимеров из расплава методами дилатометрии, рассеяния деполяризованного света или сканирующей калориметрии. [1]
Значения параметров уравнения ( 2), описывающего напряженное и деформированное состояние стеклопластиков, зависит от аналогичных характеристик связующего. Поэтому для решения проблемы получения армированных пластиков с заданными свойствами необходимо всестороннее исследование физико-механических характеристик стекловолокна и связующих и создание теории расчета, позволяющей определять характеристики армированных систем на основании известных свойств исходных компонентов. [2]
Бифуркационным называется значение параметра уравнения, при котором меняется качественная картина фазовых кривых на фазовой плоскости. [3]
Метод расчета значений параметров уравнения для чистых веществ является основополагающим в данной задаче и, в основном, определяет возможности уравнения состояния при описании свойств веществ. [4]
Строго говоря, значения параметров уравнения (3.7) следовало бы определять отдельно для каждого класса соединений, но для практических целей вполне можно ограничиться расчетом параметров только для определенной окислительной среды, полагая, что, значения общих параметров различных классов веществ являются неизменными. [5]
Равновесный состав или значения параметров уравнения могут быть найдены при помощи диаграмм, приведенных на рис. 7.7 - 7.13. Однако уравнение UNIQUAC нельзя представить таким простым способом. Поскольку параметры всех уравнений известны, если известны коэффициенты активности при бесконечном разбавлении, в целях единообразия на осях координат во всех случаях откладываются значения последних. [6]
Найденные таким образом значения параметров уравнения (4.20) могут быть использованы для оценки изменений энтальпии Я, энтропии 5и свободной энергии С, сопровождающие переход полимера в граничные слои. [7]
Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. [8]
Учитывая количество и разнообразие углеводородов данной группы, значения параметров уравнения состояния для этих веществ представлены не в виде табличных значений, а рассчитываются по универсальным корреляционным зависимостям. [9]
Исходя из известных сведений о рассматриваемом процессе, необходимо произвести оценку значений параметров уравнений математической модели, имея в виду возможность последующего уточнения их величины. Этот путь одновременно позволяет проводить более глубокое изучение моделируемого процесса и является наиболее эффективным в настоящее время, когда наши знания о процессах разделения еще далеки от совершенства. [10]
Если закономерность распределения угля по крупности установлена, то гранулометрический состав определяется значениями параметров уравнения характеристики крупности. [11]
На основании экспериментальных данных, представленных в табл. 1, графическим путем были рассчитаны значения параметров аи уравнения Фроста. Значения параметра а, пропорционального константе скорости, с повышением температуры закономерно возрастают. В равных условиях наибольшая скорость гидрогенолиза наблюдается для меркаптанов, наименьшая - для тиофенов и сульфидов. [12]
Функции f ( t) и g ( t) имеют различный вид в зависимости от значений параметров уравнения. Выделим пять возможных случаев, ниже ( 7i, С2 - произвольные постоянные. [13]
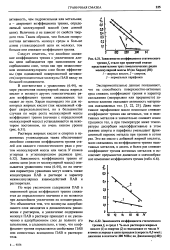 |
Зависимости коэффициента статического.| Зависимости коэффициента статического. [14] |
Зависимость коэффициента трения от длины цепи ( или от молекулярной массы) описывается уравнением типа (6.44), но на значения параметров уравнения могут влиять также концентрации ПАВ в растворе и характер межмолекулярных взаимодействий ПАВ и растворителя. [15]
Страницы: 1 2