Реакция - вид
Cтраница 3
II, § 1), для решения первого уравнения системы дифференциальных уравнений скоростей реакций вида dy / dr - k xy необходимо к заменить через у с помощью материального баланса стехиометрических уравнений на молекулярном уровне. [31]
 |
Трубчатый реактор с аксиальным переносом тепла и массы. граничные условия типа Данквертса. [32] |
Предположим, далее, что в реакторе протекает реакция первого порядка, описываемая выражением для скорости реакции вида & хсехр ( - E / RT) ( Е - энергия активации, R - газовая постоянная) и с тепловым эффектом ( энтальпией реакции) - ЛЯГ. Мы будем считать, что плотность теплового потока через стенку трубки определяется выражением 4U ( T - Tc) / d, где U - соответствующий коэффициент теплопередачи, d - диаметр трубки и Тс - температура теплообменной ( например, охлаждающей) среды вне трубки. [33]
Примем, как и при анализе компенсационного эффекта, что переход в активное состояние для некоторой серии реакций вида q или q обусловлен одной нормальной реакцией, одинаковой для всех членов соответствующей серии. [34]
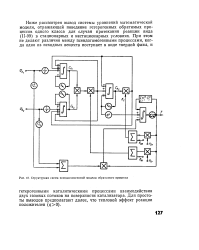 |
Структурная схема псевдогомогенной модели обратимого процесса. [35] |
Ниже рассмотрен вывод системы уравнений математической модели, отражающей поведение гетерогенных обратимых процессов одного класса для случая протекания реакции вида ( П-99) в стационарных и нестационарных условиях. [36]
Под действием жестких у-квантов ( с энергией до нескольких сот мегаэлектрон-вольт, получаемых, например, торможением электронов, ускоренных на бетатроне) идут также реакции вида ( у, 2п), ( у, р), ( у, рп), ( у, 2р), - ( Y, an) и более сложные с вылетом нескольких нуклонов из сильно возбужденного ядра. [37]
Другими словами, среднее время, в течение которого ион будет двигаться до того, как он прореагирует с другим ионом, будет порядка 1 мин для реакции вида D-D и порядка 1 сек для реакции вида T-D. Отсюда ясно, что когда объем, занимаемый горячим газом, имеет умеренные размеры, ионы, будут уходить из него, не успев прореагировать, если они не будут каким-либо способом удержаны в пределах объема. Стенки сосуда не могут быть использованы для этой цели, так как их материал перешел бы при этом в газообразное состояние. Столкновения с другими частицами при принятых нами давлениях тоже не могут привести к желаемому результату. Если бы дело шло об электрически нейтральных частицах, этот вопрос, возможно, не удалось бы разрешить. Однако так как реагирующие частицы положительно заряжены, остается возможность удержать их с помощью электромагнитного поля. [38]
При изокинетической температуре все AG - 0; константы скорости всех реакций вида q должны были бы быть одинаковыми и равными KinekbT / h, если при Т - В в данной системе реакции вида q могли бы протекать. [39]
Другими словами, среднее время, в течение которого ион будет двигаться до того, как он прореагирует с другим ионом, будет порядка 1 мин для реакции вида D-D и порядка 1 сек для реакции вида T-D. Отсюда ясно, что когда объем, занимаемый горячим газом, имеет умеренные размеры, ионы, будут уходить из него, не успев прореагировать, если они не будут каким-либо способом удержаны в пределах объема. Стенки сосуда не могут быть использованы для этой цели, так как их материал перешел бы при этом в газообразное состояние. Столкновения с другими частицами при принятых нами давлениях тоже не могут привести к желаемому результату. Если бы дело шло об электрически нейтральных частицах, этот вопрос, возможно, не удалось бы разрешить. Однако так как реагирующие частицы положительно заряжены, остается возможность удержать их с помощью электромагнитного поля. [40]
В основе этих реакций возможно лежит другой механизм. Так некоторые реакции вида 2 протекают по ионному цепному механизму, а реакции вида 3 по еще не выясненному механизму реакций ненасыщенных циклов. [41]
 |
Нахождение кинетических констант логарифмированием уравнений кинетики. [42] |
Весьма удобным приемом для оценки дифференциальным методом порядка реакции и константы скорости реакции является логарифмирование дифференциального уравнения с последующим построением логарифмического графика в координатах: скорость реакции wr - концентрация с. Предположим, что изучается реакция вида: аА ЬВ - продукты. [43]
 |
Нахождение кинетических констант логарифмированием уравнений кинетики. [44] |
Весьма удобным приемом для оценки дифференциальным методом порядка реакции и константы скоростя реакции является логарифмирование дифференциального уравнения с последующим построением логарифмического графика в координатах: скорость реакции wr - концентрация с. Предположим, что изучается реакция вида: аА ЬВ - - продукты. [45]
Страницы: 1 2 3 4