Апериодический регулятор
Cтраница 2
Из сравнения качества управления следует, что переходный процесс в разомкнутой системе при ступенчатом изменении установившегося состояния может существенно отличаться от переходного процесса самого объекта управления, если очень большие изменения, входной переменной должны быть исключены. При больших отклонениях управляющей переменной, что характерно для апериодических регуляторов, можно достичь меньшего времени регулирования. Однако это ведет к увеличению чувствительности системы к величине запаздывания. Поэтому в общем случае применять апериодические регуляторы для объектов с большим запаздыванием не рекомендуется. [16]
Поэтому обобщенный компенсационный регулятор может применяться только для объектов, нули и полюса которых расположены на плоскости z внутри окружности единичного радиуса. В частных случаях эти условия могут не выполняться, например для апериодических регуляторов и регуляторов-предикторов. [17]
Малые изменения АВ ( z) мало влияют на устойчивость системы. Следовательно, нули объекта могут располагаться вне единичной окружности на плоскости z, поскольку в случае апериодических регуляторов они не компенсируются. [18]
Для управления объектами с большим запаздыванием пригодны параметрически оптимизируемые регуляторы, описанные в гл. При этом структура параметрически оптимизируемых регуляторов типа inP - j остается той же, однако их параметры могут существенно измениться. Апериодические регуляторы AP ( v) и AP ( v l) для объектов с запаздыванием уже были рассмотрены ранее. Для регуляторов состояния способ введения запаздывания в векторно-матричную модель объекта управления играет существенную роль. Этот раздел содержит дополнения к методам синтеза регуляторов, изложенным выше. [19]
Регуляторы с конечным временем установления переходных процессов - апериодические регуляторы - описаны в гл. Метод их синтеза характеризуется весьма малыми вычислительными затратами. Модифицированные апериодические регуляторы повышенного порядка особенно пригодны в адаптивных системах управления. [20]
Затраты на синтез состоят из потребной памяти и времени вычислений при синтезе алгоритмов управления. Цифры, приведенные в табл. 11.3.2, получены для вычислителя Хьюлетт-Паккард HP 2100A с ферритовой памятью объемом 24К, внешней дисковой памятью и аппаратурно реализованной арифметикой с плавающей запятой. Время вычислений является наименьшим при синтезе апериодических регуляторов, средним при синтезе регуляторов состояния и наибольшим для параметрически оптимизируемых регуляторов. Заметим, что для параметрической оптимизации использован метод Хуки - Дживса, для которого нужен относительно малый объем памяти. Требуемый объем памяти для синтеза распределяется аналогично времени вычислений: наименьший для апериодических регуляторов, средний для регуляторов состояния и наибольший для параметрически оптимизируемых регуляторов. [21]
Регуляторы входа / выхода имеют порядки v m и n m d, если они являются структурно оптимизированными по отношению к объекту. Порядки характеристических уравнений и, следовательно, число полюсов для разных регуляторов различны. Наименьшее число полюсов равно ( m d) для точно настроенного апериодического регулятора. Для линейных объектов в общем случае пригодны обобщенные линейные и параметрически оптимизируемые регуляторы. Апериодические регуляторы и регуляторы-предикторы могут использоваться только для объектов, полюса которых лежат внутри окружности единичного радиуса на плоскости z, а обобщенные компенсационные регуляторы - только для объектов, полюса и нули которых расположены внутри единичной окружности. Порядок соответствующих характеристических уравнений также равен ( m d) и является наименьшим по сравнению с другими регуляторами входа / выхода, за исключением апериодических регуляторов. Это преимущество, однако, не реализуется, если необходимо использовать наблюдатель. Регуляторы состояния применимы к весьма широкому классу объектов управления. [22]
Межтактовые колебания, которые могут возникать в системе, включающей в себя компенсационные регуляторы ( см. гл. Джури [7.1, 2.3] назвал такой характер протекания процессов апериодическим. При ступенчатом изменении задающей переменной входной и выходной сигналы объекта должны при этом принимать новое установившееся значение после определенного конечного интервала времени. Ниже описаны методы проектирования апериодических регуляторов, которые весьма просто выводятся и требуют при синтезе небольшого объема вычислений. [23]
Из сравнения качества управления следует, что переходный процесс в разомкнутой системе при ступенчатом изменении установившегося состояния может существенно отличаться от переходного процесса самого объекта управления, если очень большие изменения, входной переменной должны быть исключены. При больших отклонениях управляющей переменной, что характерно для апериодических регуляторов, можно достичь меньшего времени регулирования. Однако это ведет к увеличению чувствительности системы к величине запаздывания. Поэтому в общем случае применять апериодические регуляторы для объектов с большим запаздыванием не рекомендуется. [24]
Для объектов с чистым запаздыванием ПИ-регулятор 2ПР - 2, относящийся к классу регуляторов с параметрически оптимизируемыми алгоритмами управления, обладает несколько лучшим качеством управления по сравнению с ПИД-регулятором ЗПР-3, поскольку характеризуется меньшей колебательностью регулируемой и управляющей переменных. Введение весового коэффициента г0 при управляющей переменной оказывает незначительное влияние на качество регулирования. Чувствительность этих параметрически оптимизируемых регуляторов к неточному заданию величины запаздывания оказывается меньшей, чем для любых других регуляторов. Наилучшее возможное качество переходного процесса по регулируемой переменной достигается в системе с апериодическим регулятором AP ( v) или с идентичным ему регулятором-предиктором РПР. Модифицированный апериодический регулятор AP ( v l) позволяет достичь нового установившегося состояния на такт позже. Однако и апериодический регулятор, и регулятор-предиктор не рекомендуется использовать в том случае, когда запаздывание в объекте известно не точно, поскольку при отличии реального и принятого при синтезе запаздывания система становится неустойчивой. Хорошее качество управления обеспечивает регулятор состояния с наблюдателем. [25]
Регуляторы входа / выхода имеют порядки v m и n m d, если они являются структурно оптимизированными по отношению к объекту. Порядки характеристических уравнений и, следовательно, число полюсов для разных регуляторов различны. Наименьшее число полюсов равно ( m d) для точно настроенного апериодического регулятора. Для линейных объектов в общем случае пригодны обобщенные линейные и параметрически оптимизируемые регуляторы. Апериодические регуляторы и регуляторы-предикторы могут использоваться только для объектов, полюса которых лежат внутри окружности единичного радиуса на плоскости z, а обобщенные компенсационные регуляторы - только для объектов, полюса и нули которых расположены внутри единичной окружности. Порядок соответствующих характеристических уравнений также равен ( m d) и является наименьшим по сравнению с другими регуляторами входа / выхода, за исключением апериодических регуляторов. Это преимущество, однако, не реализуется, если необходимо использовать наблюдатель. Регуляторы состояния применимы к весьма широкому классу объектов управления. [26]
Следует, однако, отметить, что рассмотренный метод задания полюсов обеспечивает лишь желаемое поведение изолированных собственных движений замкнутой системы. Что же касается их взаимного влияния и парирования внешних возмущений, то этого предложенный подход не учитывает. Поэтому в общем случае следует отдавать предпочтение тем методам синтеза, в которых управляющая и регулируемая переменные вычисляются непосредственно. Преимущество же рассмотренного метода состоит в том, что зависимость коэффициентов at характеристического уравнения от изменения постоянных ki обратной связи представлена в явном виде. Такой апериодический регулятор с управлением по состоянию будет рассмотрен в разд. [27]
Для объектов с чистым запаздыванием ПИ-регулятор 2ПР - 2, относящийся к классу регуляторов с параметрически оптимизируемыми алгоритмами управления, обладает несколько лучшим качеством управления по сравнению с ПИД-регулятором ЗПР-3, поскольку характеризуется меньшей колебательностью регулируемой и управляющей переменных. Введение весового коэффициента г0 при управляющей переменной оказывает незначительное влияние на качество регулирования. Чувствительность этих параметрически оптимизируемых регуляторов к неточному заданию величины запаздывания оказывается меньшей, чем для любых других регуляторов. Наилучшее возможное качество переходного процесса по регулируемой переменной достигается в системе с апериодическим регулятором AP ( v) или с идентичным ему регулятором-предиктором РПР. Модифицированный апериодический регулятор AP ( v l) позволяет достичь нового установившегося состояния на такт позже. Однако и апериодический регулятор, и регулятор-предиктор не рекомендуется использовать в том случае, когда запаздывание в объекте известно не точно, поскольку при отличии реального и принятого при синтезе запаздывания система становится неустойчивой. Хорошее качество управления обеспечивает регулятор состояния с наблюдателем. [28]
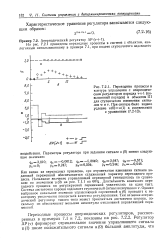
Как видно из переходных процессов, при ступенчатом изменении сигнала задающей переменной обеспечивается сглаженный характер переходного процесса. Система достаточно хорошо подавляет ступенчатый сигнал возмущения V. Однако выбранное начальное значение управляющей переменной и ( 0) приводит к некоторому увеличению показателя качества регулирования. Тем не менее апериодический регулятор такого типа может применяться достаточно широко, поскольку он обеспечивает меньшие амплитуды отклонений управляющей переменной. [30]
Страницы: 1 2 3